Backtracking

Backtracking

---

• Backtracking을 통해 미로에서 길을 찾는다고 생각해 보자.
  1. Dead End에 도달할 때까지 경로를 따라간다.
  2. Dead End에 도달하면 Fork지점까지 되돌아간다(Backtrack).
  3. 1에서 선택한 경로와 다른 경로를 선택한다.
• 만약 어떤 경로가 Dead End로 도달할 것을 미리 알 수 있는 sign이 있다면?
  • 특히 이런 sign이 경로의 초반부에서 발견될수록 많은 탐색 시간을 절약할 수 있다.

Backtracking Technique

• 어떤 집합에서 object의 sequence를 선택하는 문제를 해결하는데 사용된다.
• 이때, sequence는 어떠한 기준(criterion)을 만족해야 한다.
• DFS가 사용된다.(BFS를 사용할 수도 있다.)
• 전치순회(pre order traversal)를 이용한다.
• 0-1 knapsack problem등 NP-complete문제를 효율적으로 해결하는데 사용된다.

Backtracking vs Dynamic Programming

• Dynamic programming은 Solution의 부분집합이 생성된다.
• Backtracking은 생성되지 않아야 할 부분집합을 결정하는 technique이다.
• Backtracking은 Large Instance 문제 해결에 효과적이다(항상 해결 가능하지는 않다).

Backtracking Strategy

• Solution으로 도달하지 못하는 노드임이 확정되면, 부모노드를 통해 search되지 않은 child를 가지는 노드까지 되돌아간다.
  • non-promising node : 이 노드에서는 solution에 도달할 수 없다.
  • promising node : solution에 도달할 확률이 존재한다.
• Backtracking에서는 State Space Tree를 Pruning한다.
  • Pruning 이란 State Space Tree를 순회하는 것을 말한다.
    • 보통은 DFS를 이용하여 순회한다.
  • Pruning 중 어떤 노드가 non-promising임이 확인되면 Backtracking을 수행한다.
• Backtracking의 Search Space인 State Space Tree에서 configuration(x, y)와 Frontier Set F를 이용하여 Backtracking을 수행한다.
  • Configuration(x, y)
    • x : tree에서 search되지 않은 부분, 남아 있는 문제
    • y : 현재 노드까지 도달하기 위해 선택한 노드의 집합
    • 초기 configuration은 ($x$, $\phi$)로 설정된다.
      • x는 original problem instance이다.
    • configuration은 additional choice에 따라 새로운 subproblem configuration으로 확장된다.
    • Dead End에서는 Backtracking을 통해 다른 configuration으로 돌아간 뒤 탐색을 이어간다.
  • Frontier Set F
    • configuration의 집합이다.
    • 탐색 대기 노드의 집합으로 생각할 수 있다.
    • DFS를 이용한 Backtracking에서는 Stack으로 구현되며, BFS를 이용할 경우 Queue로 구현된다.

Backtracking Procedure

• 의사 코드를 통해 Backtracking Algorithm이 어떻게 구현되는지 알아보자.

  Algorithm Backtracking(x):
  	input(x) : A problem instance x for hard problem
  	output : soution for problem or "no solution" 
  	F <- {(x, 0)}
  	while (F!= 0) do
  		F에서 가장 promising한 configuration을 선택한다.
  		configuration을 subproblem configurtaion으로 확장한다.
  		확장된 configurations에 대해 simple consistency check을 수행한다.
  			"Solution Found" : return configuration(xi, yi)
  			"Dead end" : 해당 configuration을 버린다(discard)
  			"Continue" : F <- F + (xi, yi)
  	end
  	return "no solution"
  

• 이를 실제로 적용하기 위해서 아래의 사항들에 대한 정의가 필요하다.
  1. Frontier Set F로부터 The most promising configuration을 선택하는 방법에 대한 정의
  2. configuration(x, y)를 expend 하여 subproblem configuration을 만드는 방법에 대한 정의
     • 확장을 통해 모든 feasible configuration을 생성 가능해야 한다.
  3. simple consistency check에 대한 정의가 필요하다.
• 앞선 절에서 설명했듯이, Frontier set은 DFS의 경우 Stack으로 구현되며, BFS의 경우 Queue로 구현된다.
• 아래 그림은 Backtracking과정을 시각적으로 표현한 것이다.
  • Example State Space Tree
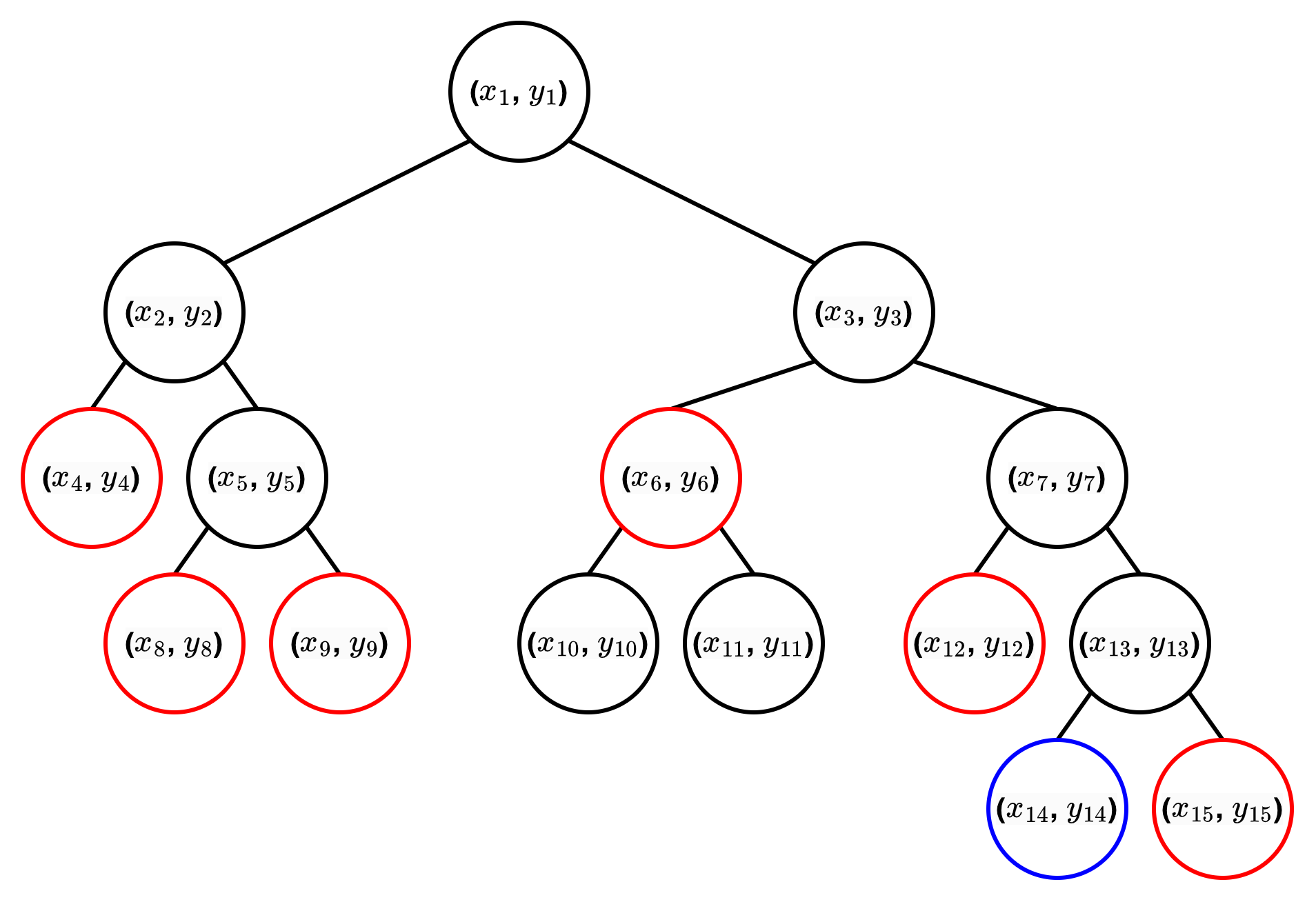
    • 붉은 테두리의 노드는 consistency check결과 non-promising으로 확인되는 노드이다.
    • 파란색 테두리의 노드는 consistency check결과 promising으로 판단되는 노드이다.
    • 이외의 노드는 Continue를 의미한다.
  • 위 트리에 대한 Backtracking중 Frontier Set F의 변화
    • F에서 stack pop된 튜플에 대해 expend를 수행한다.
    • 이 결과 생성된 모든 subproblem configuration에 대해 consistency check를 수행한다.
    • consistency check의 결과에 따라 discard, stack push, return의 동작을 수행한다.
• 이러한 방식으로 tree를 순회하면 stack의 특성상 왼쪽 노드보다 오른쪽 노드해 먼저 consistency check를 수행하게 된다. 하지만 backtracking은 결국 모든 상황에 대한 검사를 수행하기 때문에 최종적으로 정답을 탐색하는 데 문제는 없다.