Written by JS970
on
on
Backtracking - N-Queen's Problem
Backtracking - N-queen's problem
N-Queen's Problem
- N x N의 체스보드에서 N개의 퀸들이 서로를 공격하지 않도록 배치시키는 방법을 구하는 문제
- Sequence : N개의 Queen이 배치되는 위치에 대한 sequence
- Set : Queen이 위치 가능한 N*N의 공간
- Criterion : 어떠한 두 개의 Queen도 같은 행, 열, 대각선상에 존재할 수 없다.
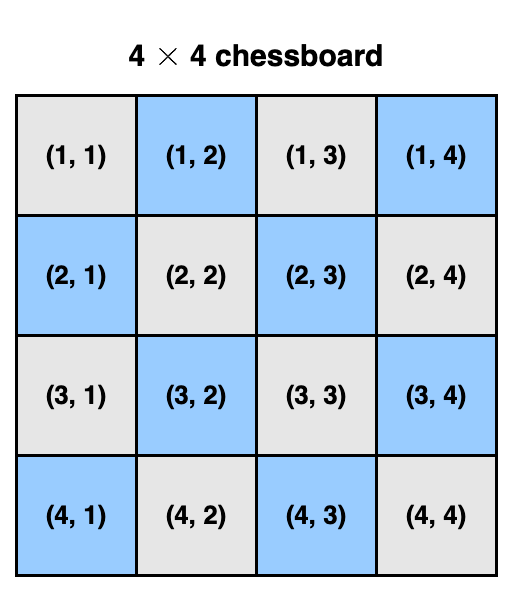
4-Queens Problem Solution
- 아래는 위 chessboard에 대해 Backtracking을 적용하여 문제를 해결하는 과정을 도식으로 나타낸 것이다.
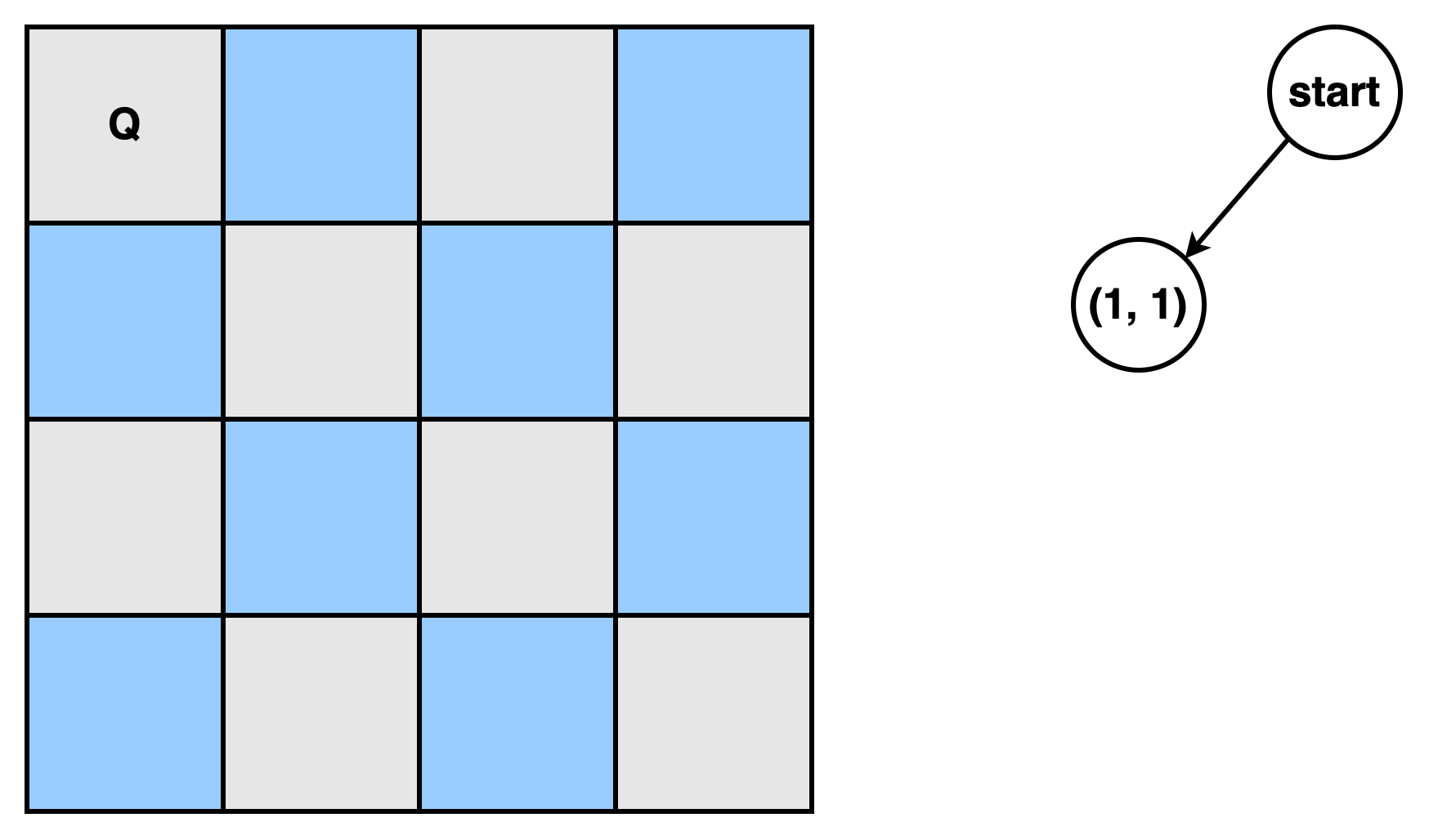
- 첫 번째 Queen배치, F = {(1, 1), $\phi$}
- F에서 most promising한 노드 선택(1, 1), 이 노드에 대해 subproblem configuration으로
expand되어 생성된 모든 노드에 대해criterion검사. 검사 결과non-promising이면 discard한다.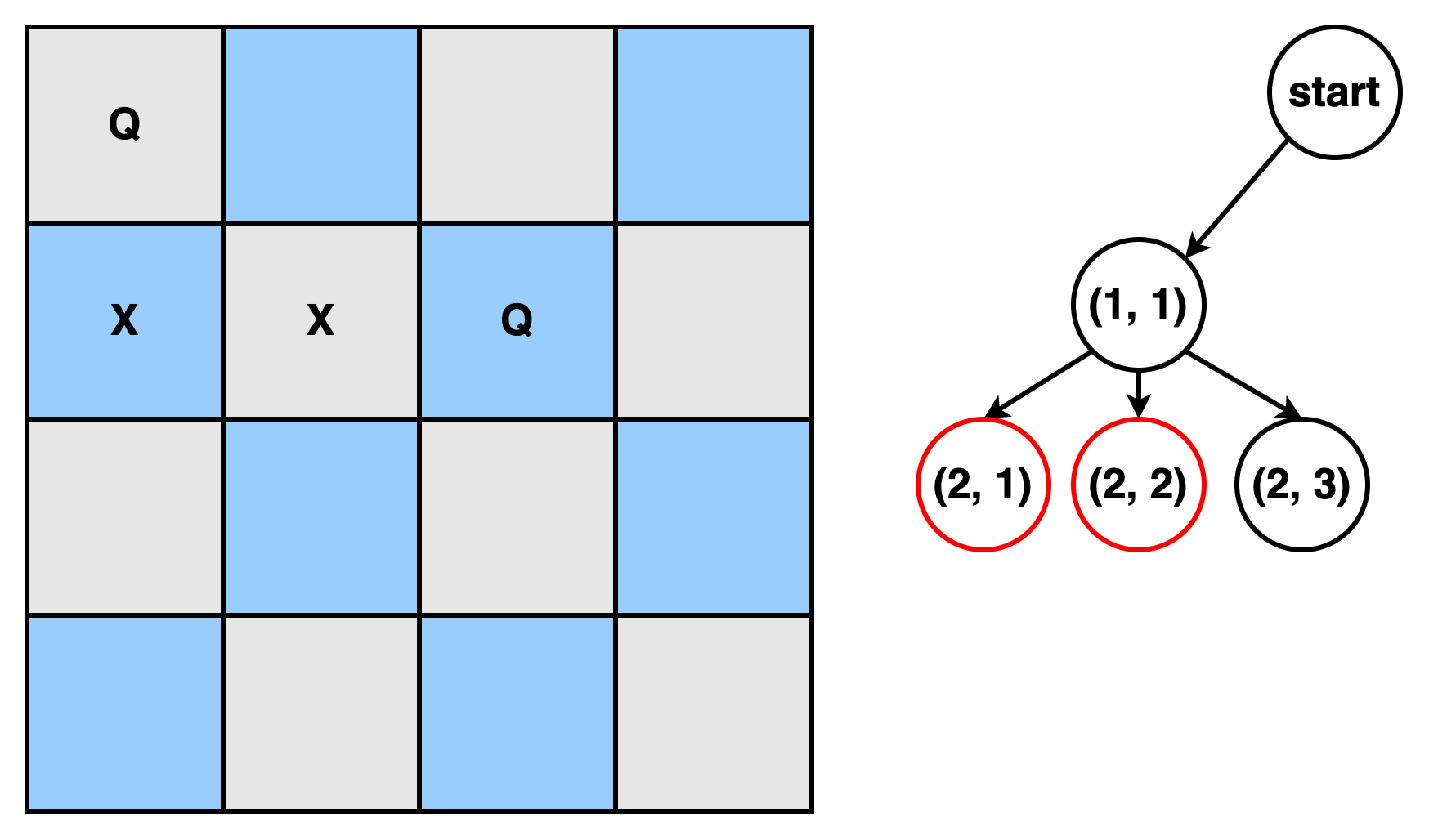
- (2, 3)의 경우
non-promising이 아니므로 F에 추가한다. 다시 subproblem configuration으로 expand 및 criterion검사를 수행한다.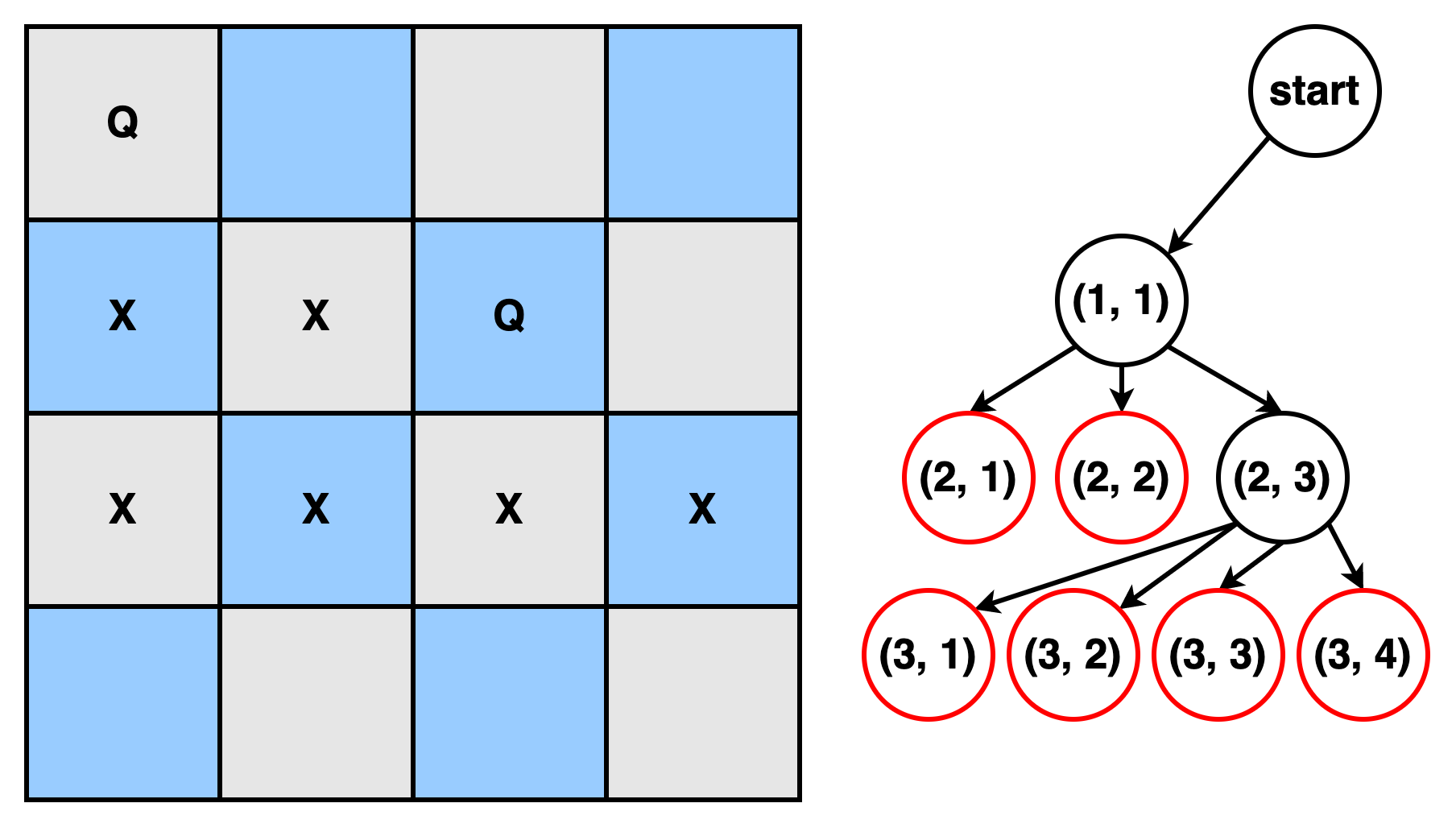
- (2, 3)의 모든 child가
non-promising이므로 Backtracking을 통해 (1, 1)까지 돌아간다. 이후 (1, 1)에서 탐색되지 않은 promising child인 (2, 4)에 대해 2의 과정을 반복한다.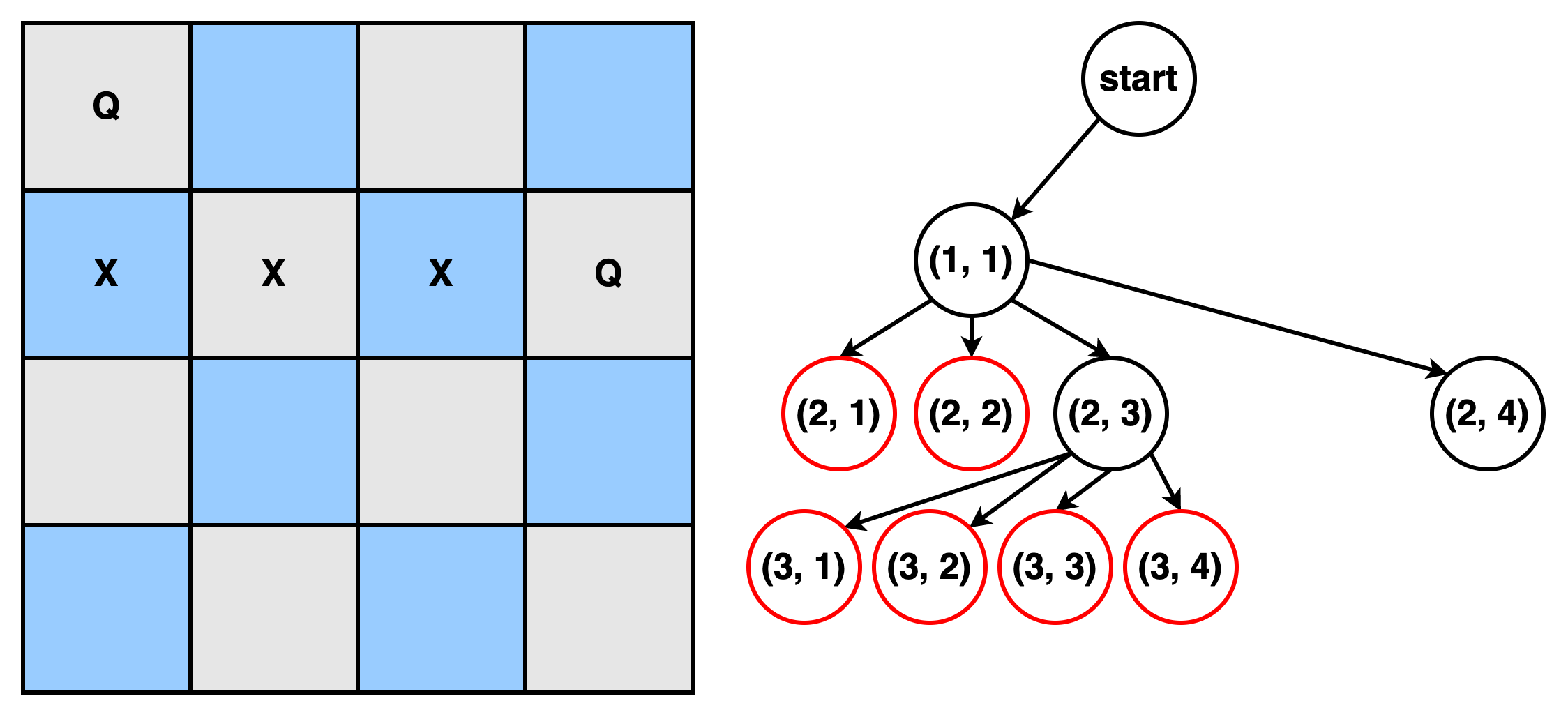
- 4에 이어서(2, 4)에 대해 알고리즘을 수행한다.
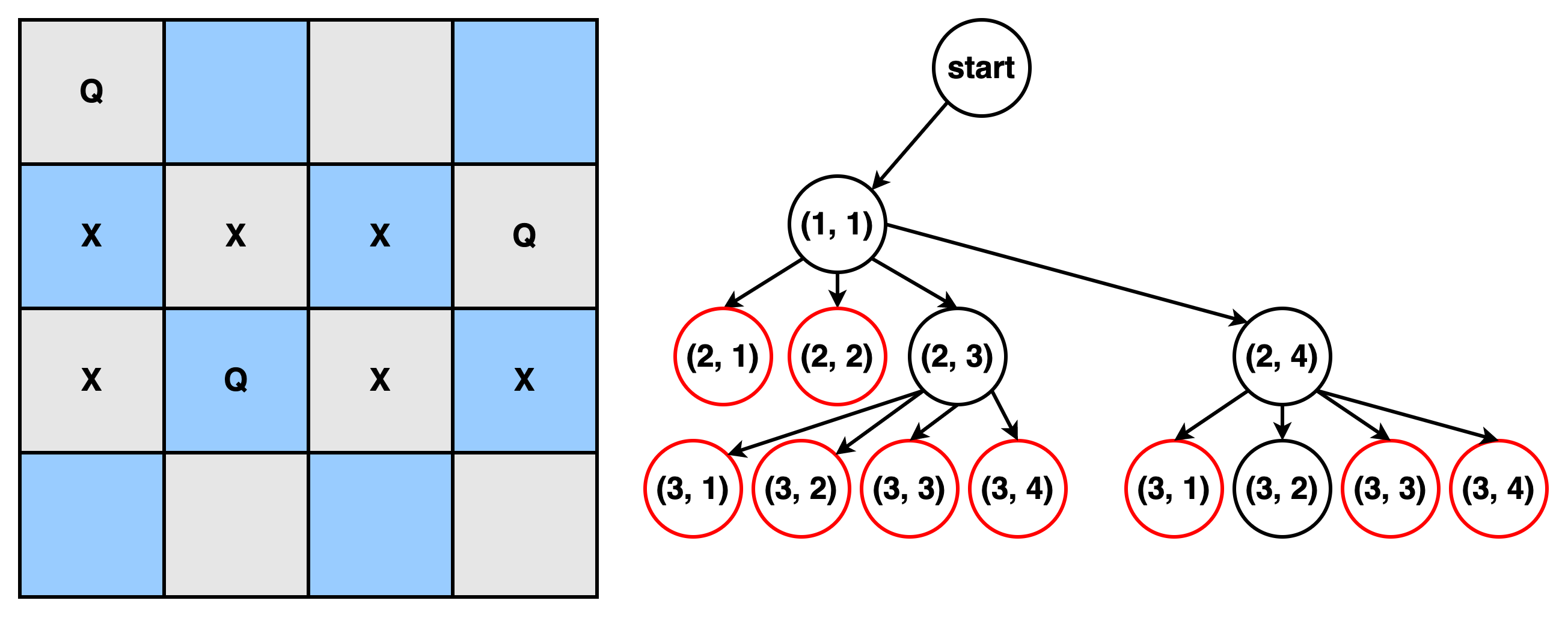
- (2,4)의 child중 promising child인 (3, 2)에 대해 알고리즘을 수행한다. 이 결과 (4, 2)가 criterion check에 의해 정답임이 판별되므로 이때의 경로 {(1, 1), (2, 4), (3, 2), (4, 2)}를 반환한다.
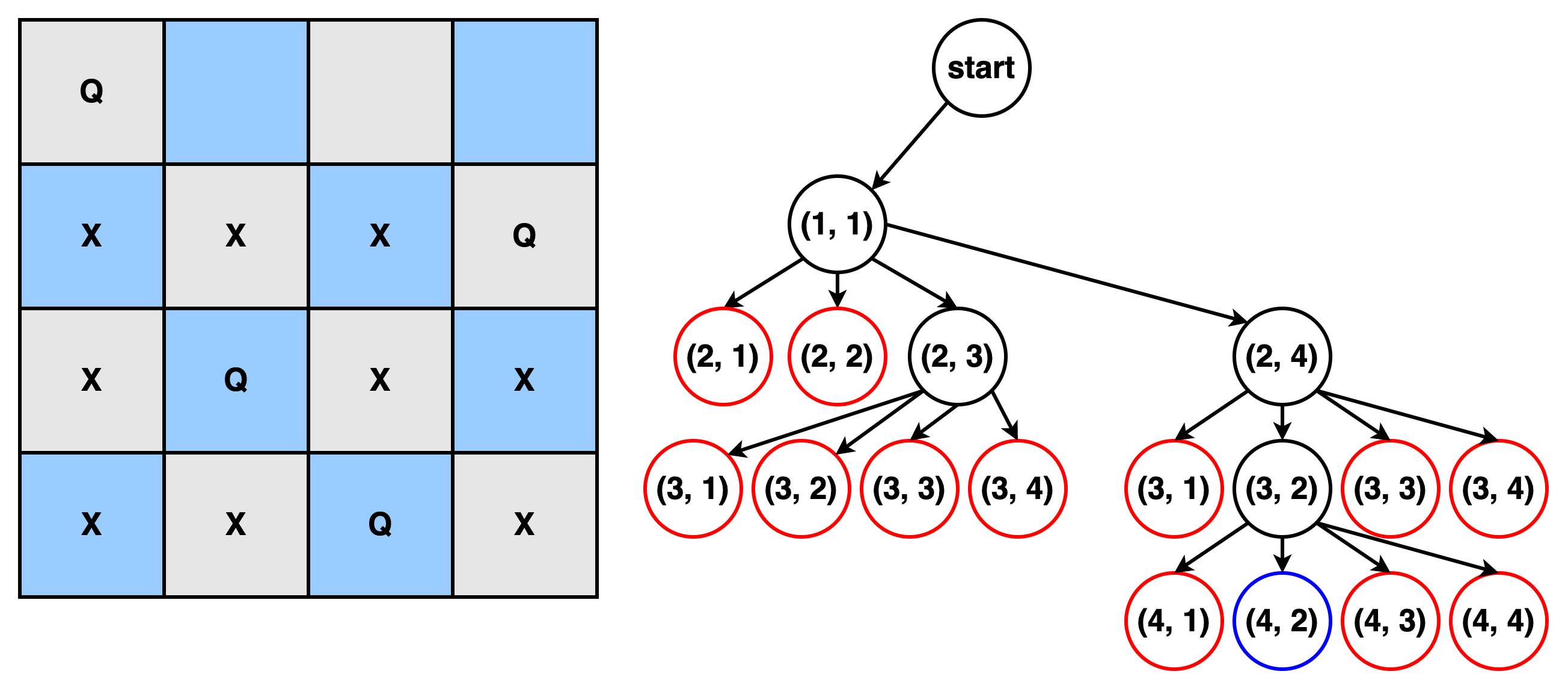
- 첫 번째 Queen배치, F = {(1, 1), $\phi$}
- 위 예시를 통해 확인할 수 있듯이, (1, 1)을 시작 노드로 가지는 4-Queens Problem의 해를 Backtracking알고리즘을 사용하면
non-promising노드의 child에 대한 조사를 생략 가능하므로 전수 조사 없이 해결 가능하다. - (1, 2), (1, 3), (1, 4)를 시작 노드로 설정하면 4-Queens Problem의 모든 해를 구할 수 있다.
Code
// TODO 2023-05-30