Backtracking - Sum of Subset Problem

Backtracking - sum of subset

---

Sum of Subset Problem

• 집합 S는 s1, s2, ... , sn의 원소로 이루어져 있다.
• W는 자연수이다.
• 이때 S의 부분집합의 원소의 합이 W가 되는 모든 경우를 찾아라
• n개의 수를 원소로 가지는 집합에서 원소의 합이 W가 되도록 하는 부분집합을 구하는 문제
• 블랙젝을 생각하면 확 와닿는다.

Promising Function

• 아래는 Sum of Subset문제를 해결하기 위한 promising function 의사 코드이다.

bool promising(int idx) {
	return (weight + total >= W) && // case 1
	(weight == W || weight + S[idx+1] <= W); // case 2
}

• weight : 현재까지 선택한 모든 원소의 합
• total : 아직 선택하지 않은 모든 원소의 합
• S[idx] : S를 오름차순으로 정렬했을 때의 idx+1번째 원소
• W : 부분집합의 합이 이 값이 된다면 찾고 있는 경우이다.
• case 1 : weight + total이 W보다 작다면 W에 도달할 수 없는 경우 배제한다.
• case 2 : weight값이 W를 초과하는 경우에 대해 배제한다.

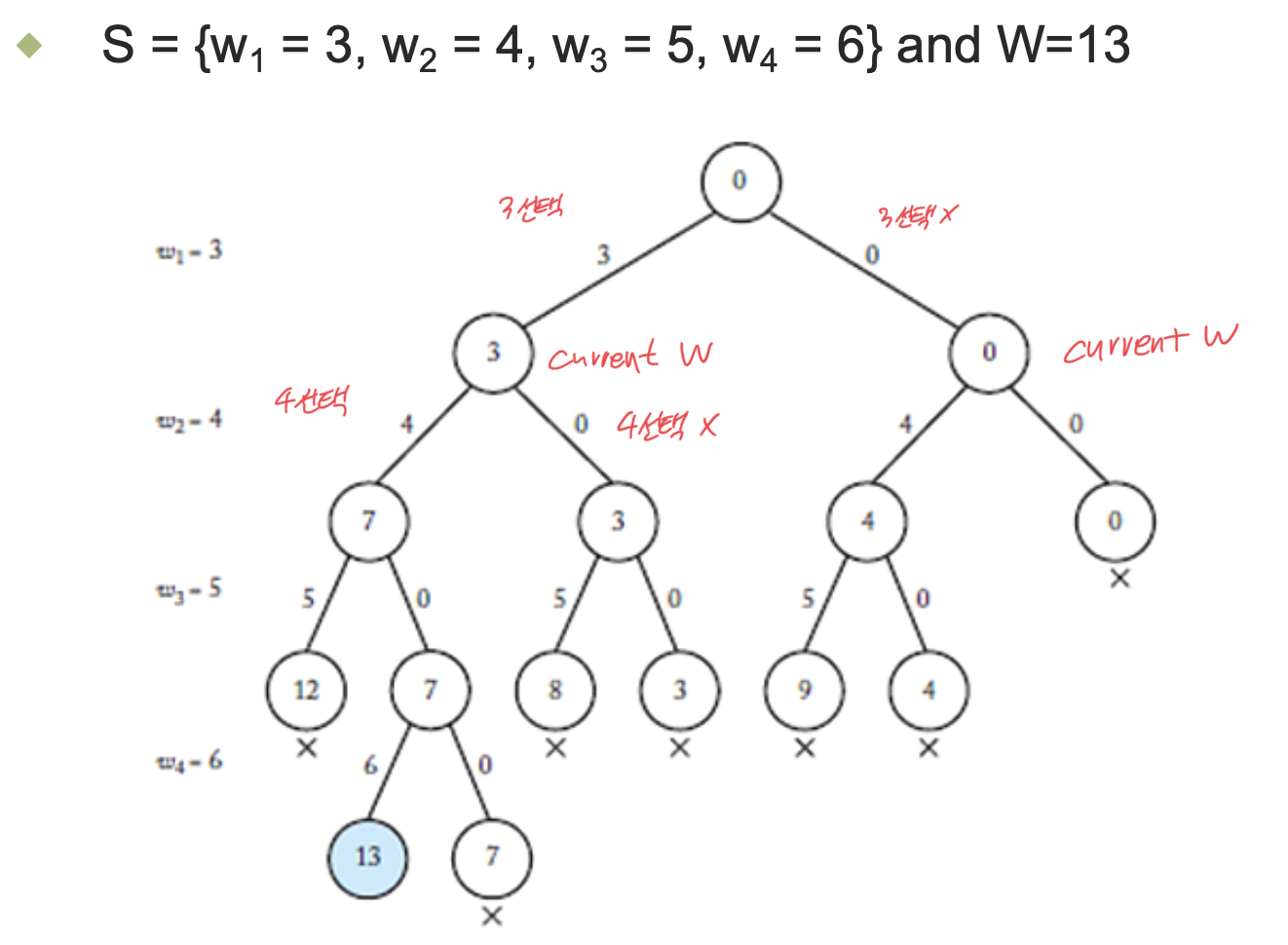
State Space Tree

• 집합 S의 원소를 오름차순으로 정렬한다.
• 오름차순으로 정렬된 S의 원소에 대해 포함시킬지, 미포함시킬지의 여부를 트리로 구현한다.
• 오름차순으로 트리를 구성하는 이유는 작은 원소를 먼저 생각하여 유망성을 판단하는 것이 유리하기 때문이다.

Solution

• 앞서 구한 promising function을 사용하여 state space tree를 promising function이 true인 노드의 서브트리에 대해서만 재귀적으로 DFS를 통해 탐색한다.
• 아래는 탐색 과정을 도식으로 나타낸 것이다.