Written by JS970
on
on
Greedy Algorithm - Kruskal Algorithm
Kruskal's Algorithm
- 그래프의 개별 노드로 구성된 V개의 subset을 생성한다.
- edge들을 weight에 따라 오름차순으로 정렬한다.
- edge를 선택했을 때 두 개의 서로 다른 V를 연결한다면, 해당 edge를 final edge set에 추가시키고, 두 V를 merge 한다.(이제 두 subset은 하나의 집합으로 인식한다.)
- subset의 집합이 하나만 남을 때까지 3을 반복해서 수행한다.
- 다음 그래프에 대해 Kruskal Algorithm을 적용해 보자.
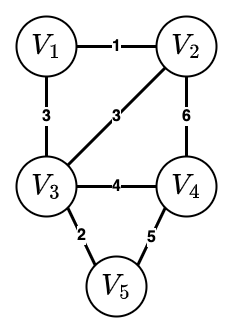
- 위에서 설명한 과정을 차례대로 수행하면 아래 그림과 같다.
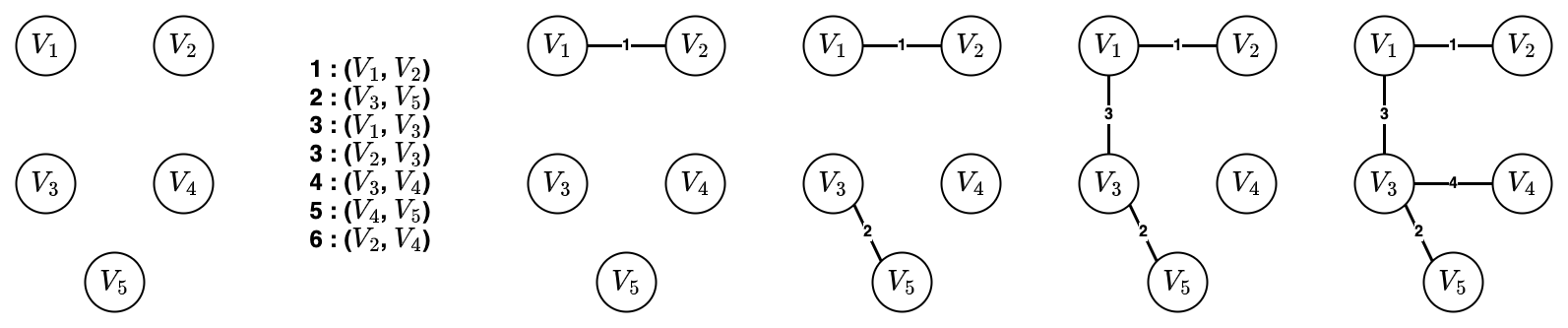
- 위에서 설명한 과정을 차례대로 수행하면 아래 그림과 같다.
Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Union-Find 자료구조를 위한 클래스
class UnionFind {
private:
vector<int> parent;
vector<int> rank;
public:
UnionFind(int n) {
parent.resize(n);
rank.resize(n, 0);
for(int i = 0; i < n; i++) parent[i] = i;
}
int find(int x) {
if(parent[x] != x)
parent[x] = find(parent[x]);
return parent[x];
}
void unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if(rootX != rootY) {
if(rank[rootX] < rank[rootY])
parent[rootX] = rootY;
else if (rank[rootX] > rank[rootY])
parent[rootY] = rootX;
else {
parent[rootY] = rootX;
rank[rootX]++;
}
}
}
};
// 간선을 나타내는 클래스
class Edge {
public:
int src, dest, weight;
Edge(int src, int dest, int weight) {
this->src = src;
this->dest = dest;
this->weight = weight;
}
};
bool compare (const Edge& a, const Edge& b) {
return a.weight < b.weight;
}
// Kruskal 알고리즘으로 최소 신장 트리를 구하는 함수
vector<Edge> kruskalMST(vector<Edge>& edges, int V) {
// 간선을 가중치의 오름차순으로 정렬
sort(edges.begin(), edges.end(), compare);
vector<Edge> result; // 최소 신장 트리를 저장할 벡터
UnionFind uf(V); // Union-Find 자료구조 객체
for(const Edge& edge : edges) {
int srcRoot = uf.find(edge.src);
int destRoot = uf.find(edge.dest);
// 사이클을 형성하지 않는다면 간선을 추가하고 Union-Find자료구조를 업데이트
if(srcRoot != destRoot) {
result.push_back(edge);
uf.unite(srcRoot, destRoot);
}
}
return result;
}
int main() {
int V, E;
cout << "정점 개수와 간선 개수를 입력하세요: ";
cin >> V >> E;
vector<Edge> edges;
cout << "간선 정보를 입력하세요 (출발 정점, 도착 정점, 가중치):" << endl;
for (int i = 0; i < E; i++) {
int src, dest, weight;
cin >> src >> dest >> weight;
edges.emplace_back(src, dest, weight);
}
vector<Edge> mst = kruskalMST(edges, V);
cout << "최소 신장 트리의 간선 정보:" << endl;
for (const Edge& edge : mst) {
cout << edge.src << " - " << edge.dest << " : " << edge.weight << endl;
}
return 0;
}
Kruskal vs Prim
- Kruskal Algorithm의 경우 모든 edge를 정렬하는 과정이 필요하다. 이때 정렬에 걸리는 시간복잡도는 mlogm이다.
- 모든 vertex가 연결된 n개의 정점을 가지는 그래프의 경우 n(n-1)/2개의 edge를 가질 수 있다.
- 따라서 kruskal algorithm의 worst case는 아래와 같다.$$\Theta(\frac{n(n-1)}2 \times log(\frac{n(n-1)}2)) = \Theta(n^2log(n^2)) = \Theta(2n^2log(n)) = \Theta(n^2log(n))$$
- V개의 vertex중 최소 edge 개수는 n-1개이다. 이때의 시간복잡도는 아래와 같다.$$\Theta((n-1)log(n-1)) = \Theta(nlogn)$$
- Prim Algorithm의 시간복잡도는 아래와 같다.$$\Theta(n^2)$$
- 따라서 edge의 개수가 많을 경우에는 Prim Algorithm이 더 빠르고, edge의 개수가 적을 경우에는 Kruskal Algorithm이 더 빠르다.