Written by JS970
on April 24, 2023

Greedy Algorithm - Prim Algorithm

Prim's Algorithm

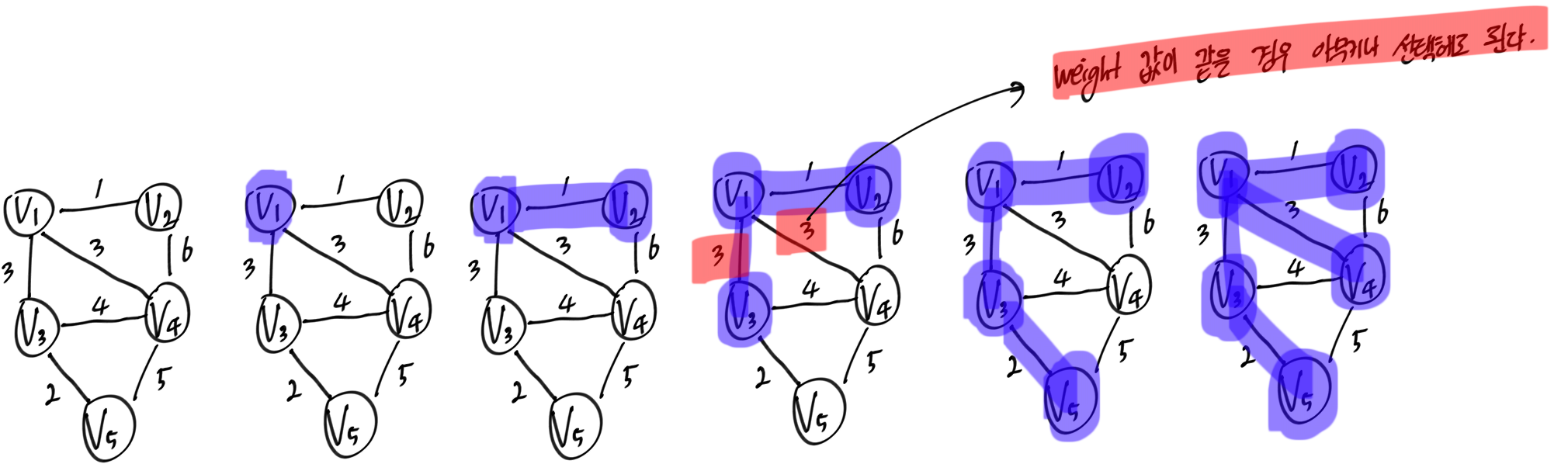
그래프에서 하나의 꼭짓점을 선택한다.
꼭짓점과 edge를 구성하는 vertex중 edge의 weight이 가장 작은 vertex를 선택한다.
2에서의 vertices와 edge를 구성하는 vertex중 edge의 weight이 가장 작은 vertex를 선택한다.
더 이상 선택되지 않은 vertex가 없을 때까지 1~3을 반복한다.

Code

/* Code by https://4legs-study.tistory.com/m/112 */
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
 
using namespace std;
 
typedef pair<int, int> p;
// number of vertex
int v = 6;
// adj[1][2][2] : e(1, 2), w = 2
vector<p> adj[7];
// check array
bool visit[7];
 
struct compare {
    bool operator()(p a, p b) {
        return a.second > b.second;
    }
};
 
void Prim() {
    // 큐 안의 간선들은 가중치 기준 오름차순으로 항상 정렬된다.
    priority_queue<p, vector<p>, compare> pque;
 
    // 출발지와 연결된 간선들을 모두 큐에 삽입
    for (int i = 0; i < adj[1].size(); i++) pque.push(adj[1][i]);
    visit[1] = true;
 
    int cnt = 0;
    // 정점의 개수 - 1만큼 반복한다.
    while(cnt < v - 1) {
        // 큐 안의 간선들 중 가중치가 가장 작은 간선을 큐에서 빼낸다.
        p curline = pque.top();
        pque.pop();
 
        // node, weight값을 curline의 값으로 갱신
        int node = curline.first;
        int weight = curline.second;
 
        // 뽑은 간선의 목적지 노드가 이미 발견된 상태라면 선택하지 않음
        if (visit[node]) continue;
        // 방문 노드 표시
        visit[node] = true;
        cnt++;
 
        // 현재 간선을 MST에 추가
        printf("%d번 정점 발견 : 비용 %d\n", node, weight);
 
        // 뽑은 간선의 목적지 노드와 연결된 간선들을 모두 큐에 삽입
        for(int i = 0; i < adj[node].size(); i++) {
            int nextnode = adj[node][i].first;
            if(!visit[nextnode]) pque.push(adj[node][i]);
        }
    }
}
 
// Graph Initialization
void init() {
    adj[1].push_back(make_pair(2, 9));
    adj[1].push_back(make_pair(3, 4));
    adj[1].push_back(make_pair(4, 3));
    adj[1].push_back(make_pair(5, 1));
 
    adj[2].push_back(make_pair(1, 9));
    adj[2].push_back(make_pair(4, 4));
    adj[2].push_back(make_pair(5, 5));
 
    adj[3].push_back(make_pair(1, 4));
    adj[3].push_back(make_pair(6, 6));
 
    adj[4].push_back(make_pair(1, 3));
    adj[4].push_back(make_pair(2, 4));
    adj[4].push_back(make_pair(5, 2));
    adj[4].push_back(make_pair(6, 8));
 
    adj[5].push_back(make_pair(1, 1));
    adj[5].push_back(make_pair(2, 5));
    adj[5].push_back(make_pair(4, 2));
 
    adj[6].push_back(make_pair(3, 6));
    adj[6].push_back(make_pair(4, 8));
}
 
int main() {
    init();
 
    printf("[MST]\n");
    Prim();
 
    return 0;
}

Every-Case Time Complexity of Prim's Algorithm

Input Size : n
서로 connection이 없는 vertex의 edge weight는 무한대로 초기화된다.
Basic operation : n-1회 반복하는 반복문 내부에 각각 n-1회 반복하는 2개의 for loop이 존재한다.
- n-1회 반복하는 반복문 : 시작 vertex를 제외한 모든 vertex에 대해 탐색
- n-1회 반복하는 for문-1 : 모든 vertex중 가장 weight이 작은 vertex 탐색
- n-1회 반복하는 for문-2 : 선택되지 않은 vertex의 weight 갱신 $$T(n) = 2 \times (n-1) \times (n-1) \in \Theta(n^2)$$

Reference

MST - Prim code

Top