컴퓨터 알고리즘 2023-03-13 수업정리

Flow

• Big $O$, Big $\Theta$, Big $\Omega$

Big $O$, Big $\Theta$, Big $\Omega$

---

Big $O$

주어진 복잡도 함수 f(n)에 대하여, n이 임의의 수 N 보다 크거나 같을 때, g(n)이 f(n)에 어떠한 상수 c를 곱한 것보다 작거나 같다면 아래와 같이 표현한다. 그리고 g(n) is oh of f(n) 이라고 읽는다. $$g(n) \leq c * f(n),\ g(n) \in O(f(n))$$

• 임의의 수 N보다 n이 커야 한다는 조건은, 입력값의 크기가 작은 경우에 더 빠른 알고리즘이 존재하므로 이러한 조건이 붙은 것이다. 당연하지만, N이 작을수록 위의 수식을 만족하기 힘들다. 하지만 어떠한 정수 N에 대해서만 만족하면 되고, Big $O$, Big $\Theta$, Big $\Omega$ 는 매우 큰 수 n에 대해서 다루기 때문에 별 의미는 없다.

Big $\Omega$

앞서 살펴본 Big $O$ 가 g(n)의 시간복잡도의 upperbound를 (g(n)은 한 f(n)보다는 빠른 알고리즘임을 의미한다.)의미했다면, Big $\Omega$ 는 g(n)의 시간복잡도의 lowerbound를 의미한다. 따라서 Big $\Omega$ 표현은 아래 수식을 만족해야 한다. 단순하게 Big $O$ notation과는 부등호 방향이 반대이다. $$if\ g(n) \in \Omega(f(n)),\ g(n) \ge c * f(n)\ for(n \ge N)$$

Big $\Theta$

g(n)이 $O(f(n),\ \Omega(f(n))$ 에 모두 속할 경우 아래와 같이 표기할 수 있다. $$g(n) \in \Theta(f(n))$$

• 결국, Big $\Theta$는 집합은 같은 시간복잡도의 집합을 표시한다고 할 수 있다.
• 정의에 따라 $2n^2,\ n^2+10$ 은 같은 Big $\Theta$는 집합에 속한다고 말할 수 있다. (same complexity를 가진다)
• Big $O$, Big $\Theta$, Big $\Omega$ notation을 통해 서로 다른 알고리즘 간의 수학적인 비교가 가능하다.
• 어떠한 시간복잡도 함수가 각 notation을 충족하는지는 부등식을 통해 증명 가능하다.

도식 표현

• 아래 그림은 각 집합의 영역을 그림으로 표시한 것이다.
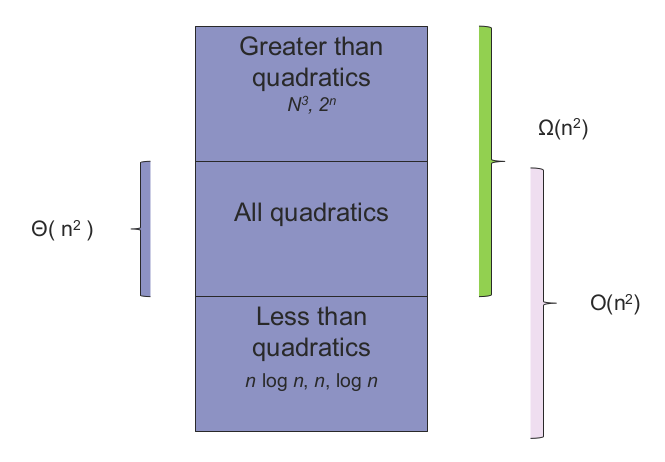
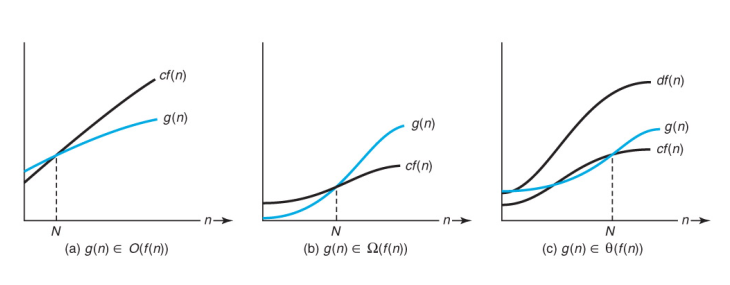
• 아래 그림은 각 집합(Big $O$, Big $\Theta$, Big $\Omega$)의 증가율을 비교한 것이다.
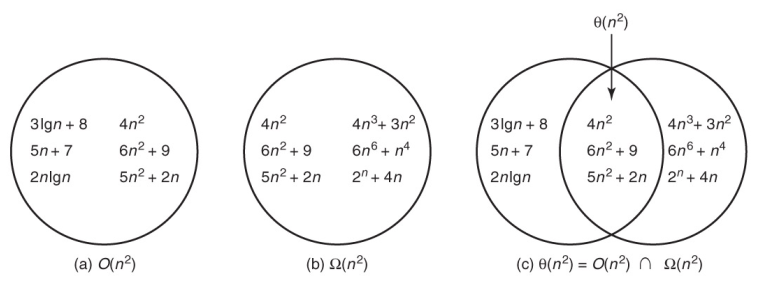
• 아래 그림은 위에서 설명한 집합에 속하는 시간복잡도 함수를 벤 다이어그램으로 표현한 것이다.

Example

아래의 수식이 참인지 증명하시오 $$n! \in \Theta(n^n)$$

• 증명의 2번 부분에서, 당연히 $log(n) \ge n/2log(n/2)$ 이지만, 임의의 상수 $c$에 대해서는 위 수식이 성립하기 때문에 참이라고 말할 수 있다.