컴퓨터 알고리즘 2023-03-15 수업정리

Flow

• Divide and Conquer - Binary Search
• Divide and Conquer - Merge Sort

Divide and Conquer - Binary Search

---

Binary Search(이진 탐색)

• 오름차순으로 정렬된 크기 n의 배열에 찾고자 하는 key값 x의 위치를 특정한다.
• 항상 중간값과 비교하여 x값이 중간값이라면 그 값의 index를 반환하고
• key 값이 중간값보다 작다면 중간값 기준 왼쪽의 subarray에 대하여 Binary Search, key값이 중간값보다 크다면 중간값 기준 오른쪽의 subarray에 대하여 Binary Search를 수행한다.
• 각 subarray로 Divide한 후 중간값에 대해 비교함으로써 Conquer하는 Divide and Conquer의 예시이다.
• recursive code

BinarySearch(int A[], key, low, high)
{
	if(high < low) return -1;
	int mid = (low + high) / 2;
	if (A[mid] > key) return BinarySearch(A, key, low, mid-1);
	else if (A[mid] < key) return BinarySearch(A, key, mid+1, high);
	else return mid;
}

• Iterative code

BinarySearch(int A[], int size, int key)
{
	int low = 0;
	int high = size-1;
	while(low <= high)
	{
		mid = (low + high) / 2;
		if(A[mid] > key) high = mid - 1;
		else if(A[mid] < key) low = mid + 1;
		else return mid;
	}
	return -1;
}

Worst-Case Complexity of Binary Search

• Binary Search에서의 주 연산은 comparison이다.
• 가장 comparison이 많이 일어나는 경우는 key값이 존재하지 않아 low <= high일 때 까지 연산을 반복하는 경우이다.
• n개의 원소를 가진 배열에 대한 complexity를 $T(n)$ 이라고 하자. 이때 Binary Search에서는 1보다 큰 모든 2의 제곱수 n에 대하여 아래와 같은 식이 성립한다. $$T(n) = T(n/2) + 1$$
• 따라서 1보다 큰 모든 2의 제곱수 n에 대하여 $T(n)$ 의 Worst-Case complexity는 아래와 같다. $$T(n) = log_2(n) + 1$$
• n이 2의 제곱수가 아닌 1보다 큰 수라면 아래와 같은 식으로 complexity를 표현할 수 있다. $$T(n) = \lfloor log_2(n) \rfloor + 1 \in \Theta(log_2(n))$$

Divide and Conquer - Merge Sort

---

Merge Sort(병합 절렬)

• 크기 n의 배열 S를 정렬하는 알고리즘이다.
• 배열 S를 n/2크기의 subarray로 Divide한다.
• 각 subarray들이 크기 1의 배열이 될때까지 반복한다.
• 두 개의 subarray를 크기순으로 merge하여 하나의 정렬된 array로 만든다.
• 말 그대로 배열을 Divide하고, divide된 배열에 대해 하나씩 merge(conquer)한다.
• 아래는 Merge Sort 과정을 나타낸 그림이다.
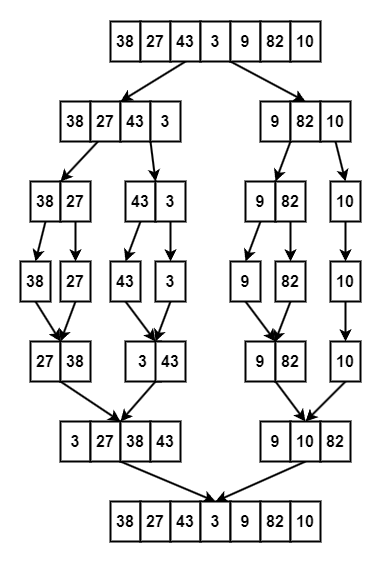
• 병합(merge)과정에 대해 자세히 살펴보면 아래와 같다.
  • 각 subarray는 이미 크기 순으로 정렬되어 있으므로 왼쪽에서 오른쪽으로 index가 이동할수록 점점 큰 값을 가지게 된다.
  • subarray - A의 첫 번째 원소와 subarray - B의 첫 번째 원소를 비교하여 더 작은 값을 새로운 merge array의 첫 번째 원소로 설정한다.
  • A, B중 원소가 선택된 subarray는 index를 증가시킨다.
  • 다시 A, B의 index가 가리키는 값을 비교하여 merge array의 다음 원소로 설정한다.
• 위의 과정을 반복하여 크기가 n인 배열에 대해 총 $\lfloor log_2(n) \rfloor$ 번의 divide과정과 merge과정에서 발생하는 n-1번의 comparison과정을 통해 배열이 정렬된다.

Worst-Case Complexity of Merge Sort

• 병합 정렬은 배열을 두 개로 나누었을 때 두 배열을 정렬하는 과정과, 두 배열을 merge하는 과정으로 나뉘어진다.
• 따라서 병합 정렬의 complexity를 $T(n)$이라고 할 때 아래와 같은 식이 성립한다. h와 m은 n개 원소를 가진 배열을 각각 h개와 m개의 원소로 가진 배열로 나누었다는 뜻이다. $$T(n) = T(h) + T(m) + (h + m - 1)$$
• 따라서 1보다 큰 2의 제곱수 n에 대해서 아래와 같은 수식이 유도된다. $$T(n) = 2T(n/2) + (n-1)$$
• 위의 수식을 바탕으로 T(n)의 시간복잡도에 대해서 아래와 같이 말할 수 있다. $$T(n) = nlog_{2}n - (n-1) \in \Theta(nlog_2n)$$
• n이 2의 제곱수가 아니라고 한다면 아래와 같다. $$T(n) = T(\lfloor n/2 \rfloor) + T(\lceil n/2 \rceil) + (n-1)$$
• 따라서 일반적으로 아래와 같은 시간복잡도를 가지게 된다. $$T(n) = n\lceil log_2n \rceil \in \Theta(nlog_2n)$$
• 증명 과정은 아래와 같다. $$n_1 = \lfloor n/2\rfloor, \ \ n_2 = \lceil n/2 \rceil$$ $$T(n) \leq T(n_1) + T(n_2) + n$$ $$\leq n1\lceil log_2n_1\rceil + n_2\lceil log_2n_2\rceil + n$$ $$\leq n1\lceil log_2n_2\rceil + n_2\lceil log_2n_2\rceil + n$$ $$= n\lceil log_2n_2\rceil + n$$ $$\leq n(\lceil log_2n\rceil - 1) + n \ \ \ (log_2n_2 \leq \lceil log_2n\rceil -1)$$ $$ = n\lceil log_2n\rceil$$