컴퓨터 알고리즘 2023-03-08 수업정리

Flow

• 알고리즘이란?
• Recursion
• 알고리즘의 분석

알고리즘이란?

---

• 문제(problem)는 "정답을 요구하는 질문"이다.
  • 배열을 크기 순으로 정렬해라
  • 값 x가 배열 S에 존재하는지 판단해라
  • 25번째 피보나치 수열은?
• 알고리즘은 "target computer"에서 소프트웨어 개발자가 주어진 입력에 대한 출력을 생성하기 위해 작성한 "logic" 이다.
• 알고리즘에서 중요하게 여겨지는 요소는 아래와 같다.
  • Correctness
  • Complexity
    • 다양한 알고리즘이 존재한다면 간단하고 빠른 알고리즘을 선호할 것이다.
    • 순차 탐색보다는 이진 탐색을 선호할 것이다.
  • Optimality
  • Clarity and Efficiency
    • 프로그램 배포 시 idea(logic)을 명확하게 설명할 수 있어야 한다.

순차 탐색(Sequential Search)

• 배열의 처음부터 끝까지 순차적으로 탐색한다.

이진 탐색(Binary Search)

• 정렬된 리스트에서 탐색하고자 하는 값이 속한 절반의 영역만을 선택하여 탐색하는 방법

Recursion

---

Recursive Fibonacci

int fib(int n)
{
	if(n<=1)
		return n;
	else
		return fib(n-1) + fib(n-2);
}

• fib(n)에서 fib(n-1), fib(n-2)를 호출한다. -> recursive
• 이렇게 recursion을 사용한다면 코드가 구현하기 쉽고 이해하기도 편하다는 장점이 있다.
• 하지만 별로 효율적이지는 않다.
• 아래는 Recursive의 문제점이다.
  • fib(5)의 값을 구하기 위해 무려 15번의 fib함수의 호출이 이루어진다.
  • 또한, 이미 구한 fib(5)의 호출로 이미 연산한 fib(3)의 값을 fib(4)를 호출하면서 다시 연산하게 된다. fib(3)뿐만이 아니라 이런 식으로 중복 연산되는 값이 상당수 존재한다.
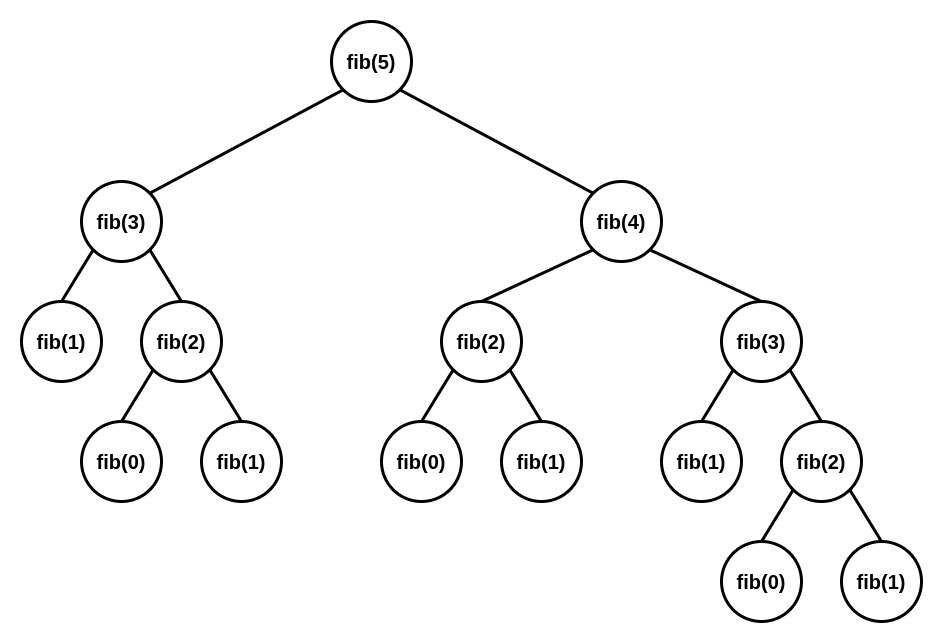
• 이렇듯 recursion은 같은 값에 대해 여러 번 연산해야 할 수 있고, 함수의 call stck이 무한정 증가할 수 있으므로 전혀 효율적이지 않다.
• 그렇다면 이러한 recursion을 피하기 위해서는 어떻게 해야 할까? -> 반복문을 사용한다.

Iterative Fibonacci

int fib2(int n)
{
	int i;
	int f[0..n];
	f[0] = 0;
	if(n > 0)
	{
		f[1] = 1;
		for(i=2; i <= n; i++)
			f[i] = f[i-1] + f[i-2];
	}
	return f[n];
}

• fib2함수에서는 fib함수와 달리 이전 값을 배열에 저장하고, 반복문을 통해 다음 피보나치 배열의 값을 저장한다.
• fib2함수는 recursion이 없으므로 단 1번의 함수 호출만 발생한다.
• 또한, fib2(5)을 5번의 연산만을 통해 계산할 수 있다.

Anyway...

• 물론 모든 경우에서 recursion이 효울적이지 않은 것은 아니다.
• 또한 recursion은 앞서 설명한 것처럼 코드가 구현하기 쉽고, 이해하기에 편리하다.
• 그렇다면 상황에 따라 recursion이 적합한 경우도 있을 텐데 이를 어떻게 알까? -> 이것이 컴퓨터 알고리즘을 공부하는 이유이다.

알고리즘의 분석

---

• 어떤 프로그램(알고리즘)이 다른 프로그램도다 효율적인지 추정하는 방법으로 실행 시간을 비교하는 방법을 생각할 수 있다. 하지만 같은 환경에서 비교가 불가능한 경우가 다수 존재한다.
• 앞선 fib, fib2함수의 경우 굳이 실행시켜보지 않더라도 직관적으로 fib2가 더 효율적임을 알 수 있다.

시간복잡도

• 함수에서의 매개변수에 따른 실행시간을 생각해 보자

function1(A[], n)
{
	k = n/2;
	return A[k];
}

• 위의 function1은 매개변수와 무관하게 일정한 실행시간을 가진다.
• 이러한 경우 Constant time의 시간복잡도를 가진다고 말한다.

function2(A[], n)
{
	sum = 0;
	for(int i = 1; i <= n; i++)
		sum += A[i];
	return sum;
}

• 위의 function2의 경우, n=1일때의 수행시간을 1이라고 한다면, n = k라면 선형적으로 k의 수행시간을 가질 것이다.
• 이는 function2의 주 연산이 덧셈, 할당이고, 매개 변수 n에 따라서 주 연산 횟수가 늘어나기 때문이다.
• 이러한 경우 n의 시간복잡도를 가진다고 말한다.

function3(A[], n)
{
	sum = 0;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
			sum += A[i]*A[j];
	return sum;
}

• function3의 경우 n에 따라 수행시간은 $n^2$ 만큼 증가할 것이다.
• 이러한 경우 $n^2$ 의 시간복잡도를 가진다고 말한다.

위에서 살펴본 시간복잡도는 세 가지 경우로 나누어 생각할 수 있다.

1. Worst case
2. Best case
3. Averge case 사실 위의 세 경우 중 Best case에 대한 시간복잡도는 별로 의미가 없으며, Worst case의 시간복잡도가 최악의 경우를 보장하기 때문에 주 관심사가 된다.

또한 아래와 같이 시간복잡도를 구분할 수 있다.

• 매개 변수 n에 대해서
  • Constant$$ 1, 3, 9, ...$$
  • Linear$$n, 2n, 3n-2, 21n+100, ... $$
  • Quadratic$$n^2, 2n^2-3, 4n^2-3n+23, ... $$
  • Cubic $$n^3 , 4n^3+3n^2-2n+7, ...$$