프로그래밍언어론 2023-03-28 수업정리

Flow

• review
• Syntax & Grammar
• Grammar Example
• Ambiguity

review

---

프로그래밍언어론 3.28 수업정리에서 이어진다.

• Basic은 1980년대의 Micro PC, GUI 등의 환경 및 GW Basic, Apple Basic을 거쳐 Visual Basic이 되었다.
• SNOBOL(문자열 처리 언어) 는 Perl에 영향을 주었다.
• LISP(심볼 처리), APL(행렬, 벡터 연산)은 이후 Haskell, ML, Scala, clojure등 함수형 언어에 영향을 주었다.
• IAL(ALGOL)은 다른 언어들과는 달리(앞서 설명한 프로그래밍 언어들은 프로그래머와 컴퓨터 간의 의사소통 목적으로 설계되었다.) 프로그래머 간의 소통을 위한 언어로 설계되었다.

Syntax & Grammar

---

• 프로그래밍 언어는 언어의 명세서(설계도)를 필요로 한다.
• 언어의 명세는 Syntax와 Semantics로 나타낸다.
  • Syntax는 Grammar(거의 표준)를 통해 표현한다.
  • Syntax는 언어의 외적인 형태를 뜻한다.
  • Semantics는 따로 표준이 정해져 있지 않으며, 자연어를 사용하여 표현한다.
  • Semantics는 프로그램의 의미를 뜻한다.

Syntax

• Language : 문장의 집합
• Sentence : 문장
• Token : 토큰(단어의 부류)
• Lexeme : 단어, 의미의 최소 단위
• 아래 C언어 코드에서 lexeme은 16개, token은 12개, 문장 1개를 확인할 수 있다.
  • lexeme : int, main, (, ), {, return, printf, (, "Hello?\n", ), ?, 0, -1, ;, }
  • token : [int], [main, printf], [(], [)], [{], [return], ["Hello?\n"], [?], [0, -1], [:], [;], [}]
  • sentence : 전체 코드

int main() {
	return printf("Hello?\n") ? 0 : 1;
}

Syntax 표기법

• Context-Free Grammar(CFG)
  • 춈스키에 의해 고안된 문법 표기법
  • (V, T, S, P)로 표기한다. (또는 (N, T, P, S))
    • V : a set of variables(nonterminals)
    • T : a set of Terminals
    • S : a designated variable
      • S $\in$ V 이다.
    • P : a set of rules
• Backus-Naur Form(BNF)
  • ALGOL58, 60의 개발에 참여한 John Backus, Peter Naur가 동시에 고안했다.
  • nonterminals에 대해 괄호를 사용하고, terminal기호에 대해 인용 기호를 사용했다.
  • 이 외에도 몇몇 기호를 추가하였다.
  • CFG와 동치이다.
  • 텍스트 표기가 가능하다.

CFG

• CFG는 rules의 집합으로 표현 가능하다.
• rule의 좌항은 nonterminal, 우항은 terminal 또는 nonterminal이다.
• 아래는 Pascal while문의 CFG 표기이다.
  • <while_stmt> -> while <bool_expr> do <stmt>
    • 좌항은 우항으로 대체 가능하다는 rule이다.
    • 좌항의 <while_stmt> 은 변수(V)이다.
    • 우항의 while, do는 상수(T) 이다.
    • 우항의 <bool_expr>, <stmt>는 변수이다.
• C의 while의 경우 아래와 같다.
  • <while> -> while (<조건식>) <문장>
• Python의 while의 경우 아래와 같다.
  • <while> -> while <조건식> : <문장>

Grammar Example

---

• 아래 CFG와 BNF는 문법 표기의 예시이다.

• 두 표현법은 서로 같은 문법을 나타내고 있다.

• 총 10개의 rules를 확인할 수 있다.

• CFG

  <prog> -> begin <stmt_list> end

  <stmt_list> -> <stmt>

    	 |  <stmt>;<stmt_list>
  

  <stmt> -> <var>:=<expr>

  <var> -> A | B | C

  <expr> -> <var>+<var>

    	 | <var>-<var>
  
    	 | <var>
  

• BNF

  <prog> ::= begin <stmt_list> end

  <stmt_list> ::= <stmt>

    	  | <stmt>';'<stmt_list> 
  

  <stmt> ::= <var>'::='<expr>

  <var> ::= 'A' | 'B' | 'C'

  <expr> ::= <var>'+'<var>

          | <var>'-'<var>
  
          | <var>
  

Derivation(유도)

• 어떠한 sentence가 well formed인지 확인해 보자.

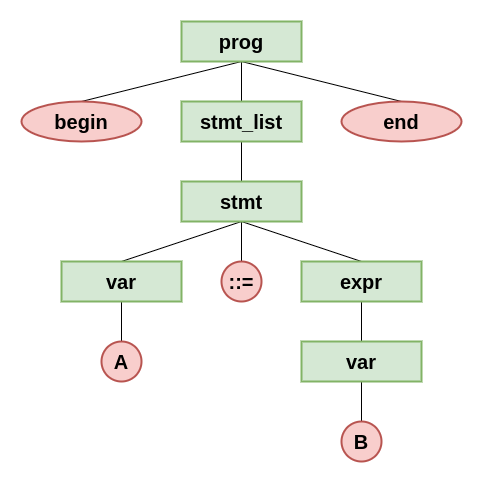
• 위의 Grammar Example에 대해서 Sentence : begin A ::= B end 는 아래와 같이 derivation된다. <prog>

  => begin <stmt_list> end

  => begin <stmt> end

  => begin <var> end

  => begin A ::= <expr> end

  => begin A ::= <var> end

  => begin A ::= B end

• 따라서 begin A ::= B end 라는 sentence는 유효한 문장이라고 결론지을 수 있다.

Parse Tree

• parse tree는 derivation을 계층적, 시각적으로 표기한 것이다.
• 변수들 중 어떤 변수를 먼저 유도했는지에 대한 순서는 무시한다.
• 바로 위의 derivation에서 확인한 sentence의 parse tree는 아래와 같다.

Ambiguity(모호성)

---

• Grammar의 속성이다.

• 같은 문법 규칙을 따른다고 하더라도 어떤 Variable에 대해 먼저 derivation을 진행했는지에 따라서 여러 가지 parse tree가 생성될 수 있다. 이 경우 "grammar is ambiguous" 이다.

• 아래와 같은 문법에서 Sentence : 2 + 3 * 5를 derivation 해 보자.

  <expr> -> <expr>+<expr>

        |  <expr>*<expr>
  
        | (<expr>)
  
        | <num>
  

  <num> -> 1 | 2 | 3 | 4 | 5

  • 주어진 sentential form은 <expr>+<expr>*<expr> 이다.
  • 하지만 이러한 sentential form에 대한 parse tree는 아래와 같이 두 가지 경우가 존재한다.
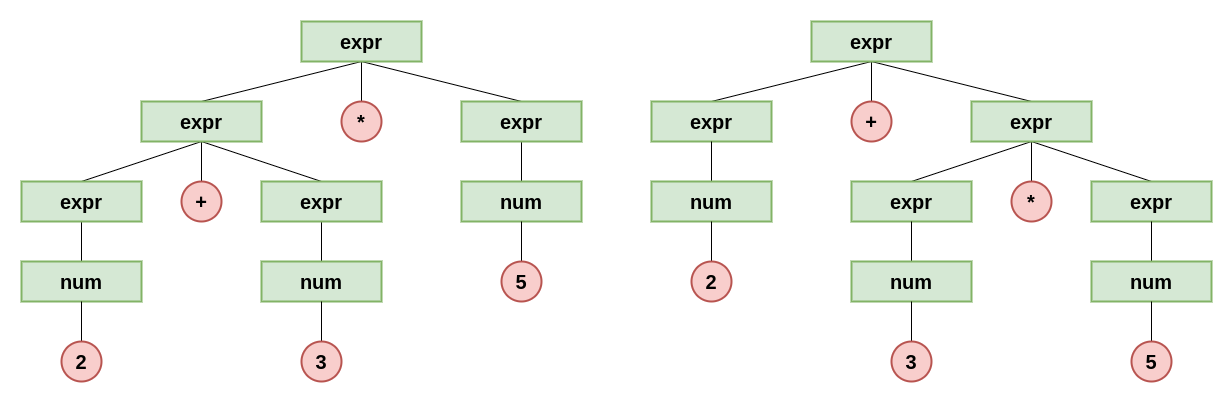
  • parse tree가 2개 존재하므로 본 grammar는 ambiguous하다.

Removing the Ambiguity

1. 결합방향을 명시한다.

   • <term> 이라는 nonterminal을 추가하여 연산자가 항상 <term>의 특정 위치에서 생성되도록 한다.

   • 아래는 연산자가 항상 <term>에 좌결합하도록 grammar를 수정한 것이다.

     <expr> -> <expr>+<term>

         | <expr>*<term>
     
         | <term>
     

     <term> -> (<expr>)

         | <num>
     

     <num> -> 1 | 2 | 3 | 4 | 5

   • 아래는 문법을 수정한 후의 Statement : 2+3*5에 대한 parse tree 중 하나이다.

   • 여전히 파스 트리는 여러 개가 나올 수 있으므로 ambiguous 하다.

2. 생성 규칙 수정을 통해 선행 연산을 설정한다.

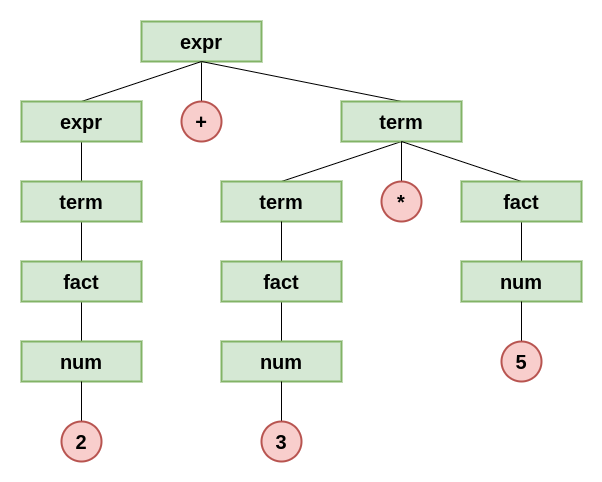
   • <fact>라는 nonterminal 기호를 추가하여 선행 연산을 설정한다.

   • +연산은 <expr>에 의해서만 생성 가능하다.

   • *연산은 <term>에 의해서만 생성 가능하다.

   • 아래는 수정한 grammar이다.

     <expr> -> <expr>+<term>

         | <term>
     

     <expr> -> <term>*<fact>

         | <fact>
     

     <fact> -> (<expr>)

         | <num>
     

     <num> -> 1 | 2 | 3 | 4 | 5

   • 아래는 문법을 수정한 후의 Statement : 2+3*5에 대한 parse tree이다.

   • 이제는 단 하나의 parse tree만 생성되므로 본 문법은 unambiguous grammar라고 말할 수 있다.

   • 참고로 이러한 방법을 통해 ambiguity를 제거하는 것을 precedence cascading이라고 한다.