Searching

Searching

---

Binary Search

• 탐색이란 key값으로 정렬된 공간에서 목표로 하는 key값을 찾는 것을 의미한다.
• Binary search는 이진 탐색이며, 탐색 공간의 중간값과 배교하여 탬색 공간을 절반으로 줄여 가며 목표로 하는 key값과 일치할 때까지 탐색을 하는 방법이다.
• tree자료구조를 사용하여 binary search와 sequential search의 탐색 횟수를 비교하면 아래와 같다.
  • Binary Search
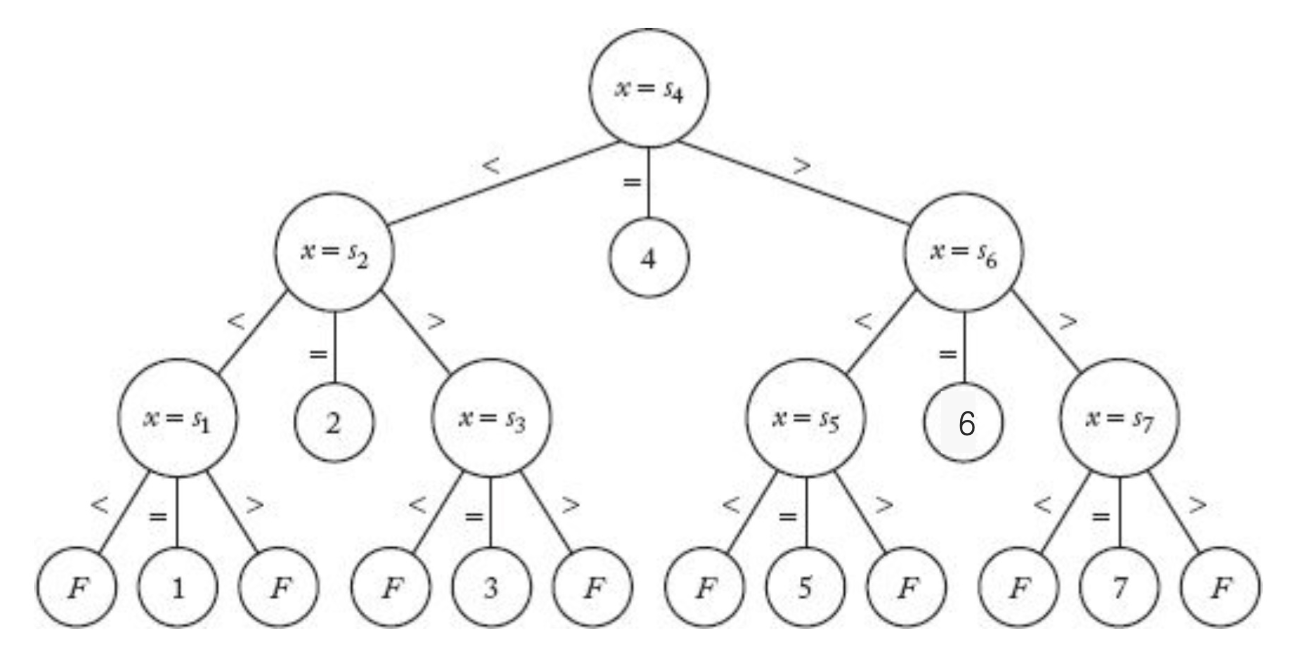
  • Sequential Search
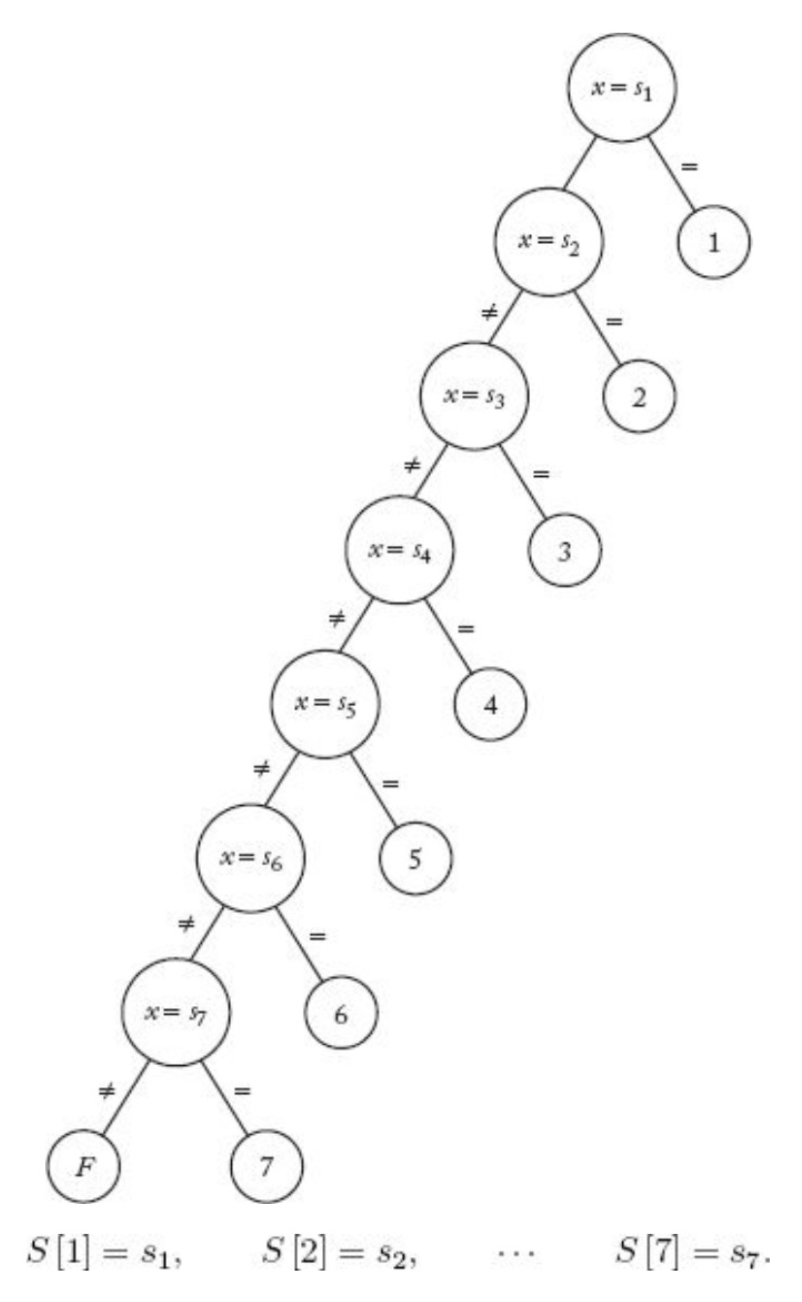
  • tree의 depth가 비교 연산의 횟수를 의미한다.
  • binary search의 경우 floor(log n)번의 비교 연산을 통해 목표 key를 찾을 수 있다.

Interpolation Search

• 보간 검색이라고도 한다.
• binary search와 비슷한 방법이지만, 중간값을 선택하는 방법에 차이가 있다.
• 보간 검색은 중간값을 선택할 때, 목표로 하는 key값의 위치를 예상하여 이 값을 중간값으로 설정한다.
• 보간 검색은 평균적으로 binary search방식에 비해 효율적이지만, 정렬된 key값이 불균일하게 분포할수록 성능이 감소한다.
• 보간 검색의 average case 시간복잡도는 log(log n) 이다.
  • 이는 binary search의 시간복잡도인 log n 보다 빠르다.
• worst case(key값이 evenly distributed되지 않은 경우)의 경우 sequential search와 비슷한 효율을 보인다.

Robust Interpolation Search

• 보간 검색의 worst case는 중간값이 계속해서 경계값(low)으로 설정되는 것이다.
• robust interpolation search에서는 중간값을 계산할 때 사용하는 사이 간격(gap)과 중간값을 아래와 같이 설정한다.$$gap = \lfloor(high - low+1)^{1/2}\rfloor$$$$mid = minimum(high-gap,\ maximum(mid,\ low+gap))$$
• robust interpolation search의 average case 시간복잡도는 log(log n) 이다.
• worst case의 경우의 시간복잡도는 ((log n) * (log n)) 이다.
• 여전히 worst case의 경우 binary search보다 효율이 떨어진다.

B-trees

• Search Time을 줄이기 위한 Data Structure이다.
• B 트리는 아래와 같은 특징을 가진다.
  1. 노드에는 2개 이상의 key값이 들어갈 수 있으며, 항상 정렬된 상태로 저장된다.
  2. 내부 노드는 m/2 ~ m개의 자식 노드를 가질 수 있다. 최대 m개의 자식을 가지는 B트리를 m차 B트리라고 한다.
  3. 특정 노드의 key가 k개라고 하면, 자식 노드의 개수는 k+1개여야 한다.
  4. 특정 노드의 왼쪽 서브 트리는 특정 노드의 key값보다 작은 값들로, 오른쪽 서브 트리는 큰 값으로 구성된다.
  5. 노드 내의 key값은 floor(m/2)-1개부터 최대 m-1개까지 포함될 수 있다.
  6. 모든 leaf node는 같은 depth(level)에 존재한다.
• 3-2 B tree에 대해 알아보자.
  • 각 노드는 한 개 혹은 두 개의 key를 가진다.
  • key가 하나인 노드의 child개수는 2개이다. key가 두 개라면 child는 3개이다.
  • 좌측 서브트리의 key들은 해당 노드의 key보다 작거나 같다.
  • 우측 서브트리의 key들은 해당 노드의 key보다 크거나 같다.
  • 모든 노드는 같은 레벨에 존재한다.
• 3-2 B tree의 삽입 과정에 대해 알아보자.
  • 아래 그림과 같은 3-2 B tree가 있다.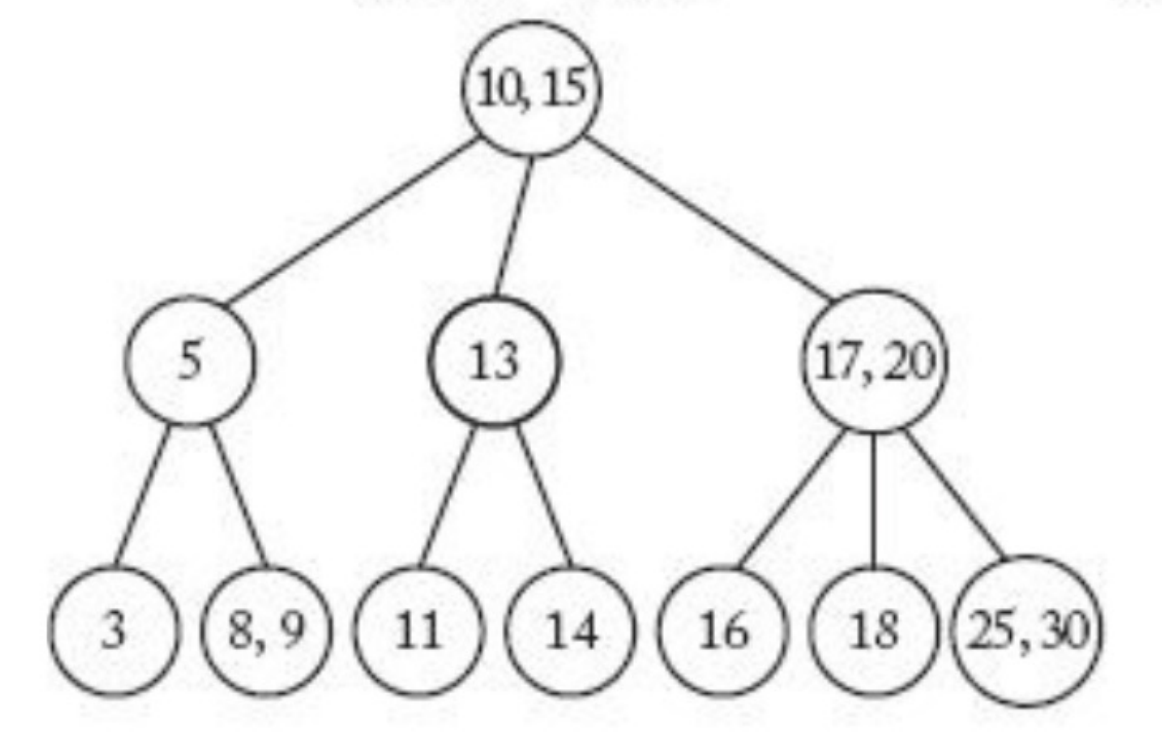
  • 이때 35가 3-2 B tree에 추가되면 가장 우측 아래에 위치하게 된다.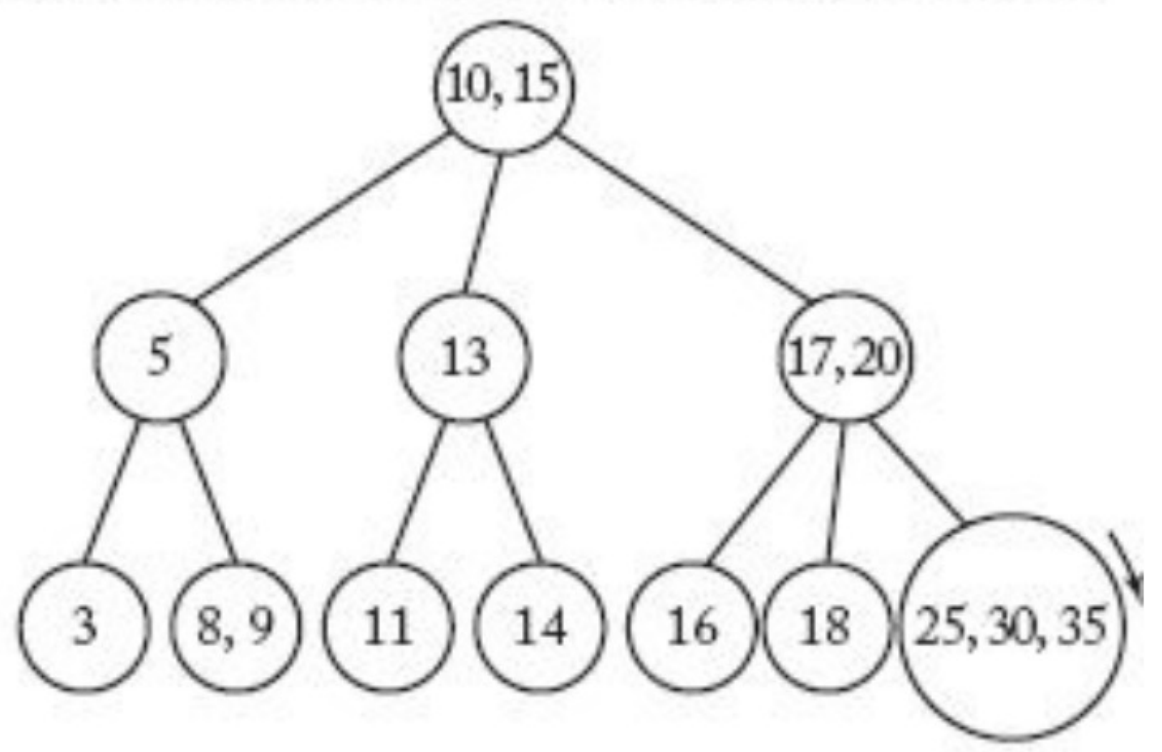
  • leaf node의 key가 3개 있다면 중간값을 부모 노드로 올리고 나머지 두 값을 자식 노드로 가진다.
  • 부모 노드의 key가 3개이고 자식 노드가 4개이다. 다시 중간값을 부모 노드로 올린다. left child는 작은 두 개의 child노드를, right child는 큰 두 개의 child노드를 상속한다.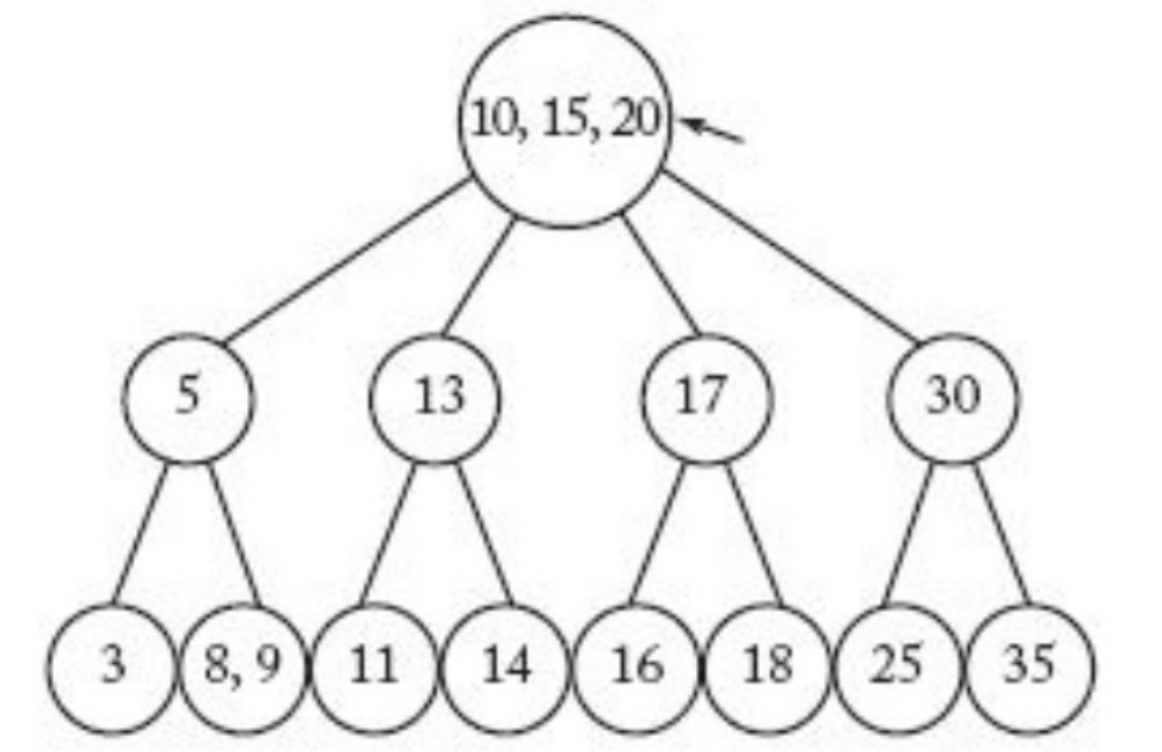
  • 루트 노드에 대해 다시 중간 값을 부모 노드로 가지도록 하면 아래와 같은 구조를 가지게 된다.
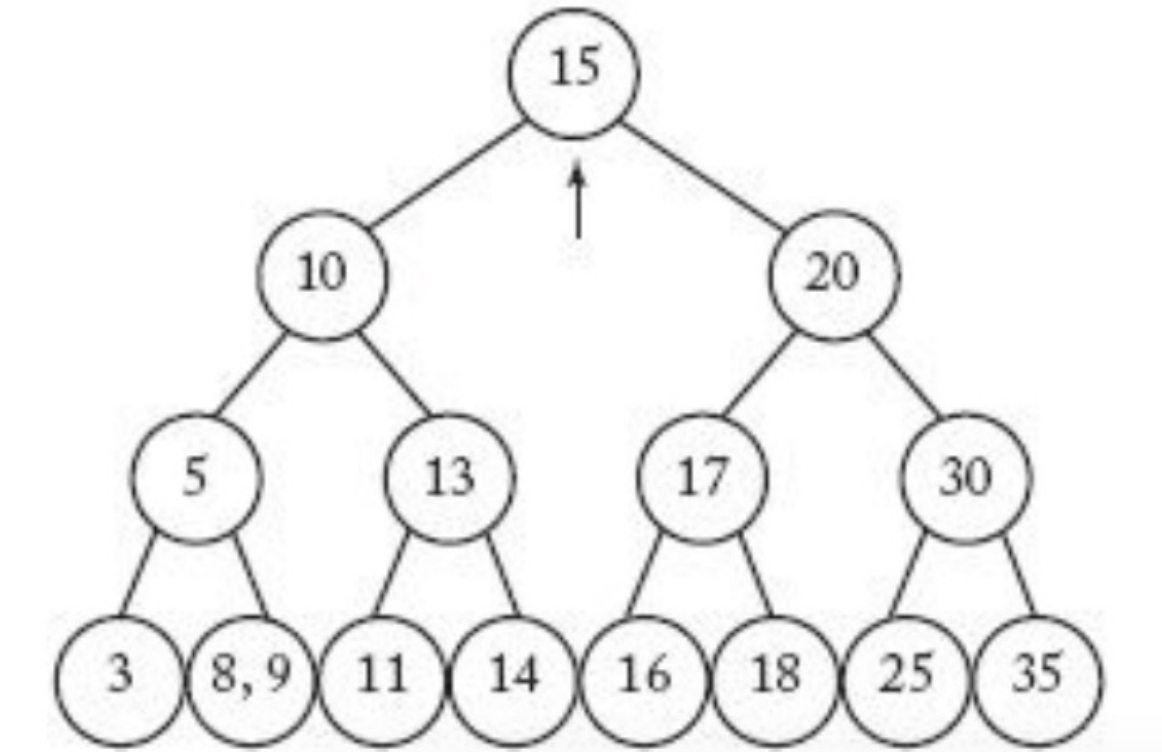
  • 이러한 과정으로 삽입이 일어나게 되면 항상 모든 leaf node의 level이 같도록 유지된다.

Red Black trees

• 균형을 알아서 맞추는 binary search tree중 하나이다.
• 아래의 조건을 만족해야 한다.
  1. 모든 노드는 red 또는 black의 색상을 가진다.
  2. 루트 노드는 항상 black이다.
  3. NIL children은 black이다.
  4. red의 자식 노드는 항상 black이다.
  5. 어떤 노드 X에서 leaf black노드까지의 경로 중 거치는 black노드 개수는 항상 같다.
• 탐색 시간은 O(log n) 이다.
• 삽입/삭제 시간은 O(log n) 이다.
• Red Black Tree의 삽입 과정에 대해 알아보자.
  • 삽입 시 새로운 노드는 항상 red이다.
  • 삽입 연산에 대해서 아래와 같은 세 가지 경우의 수가 존재한다.
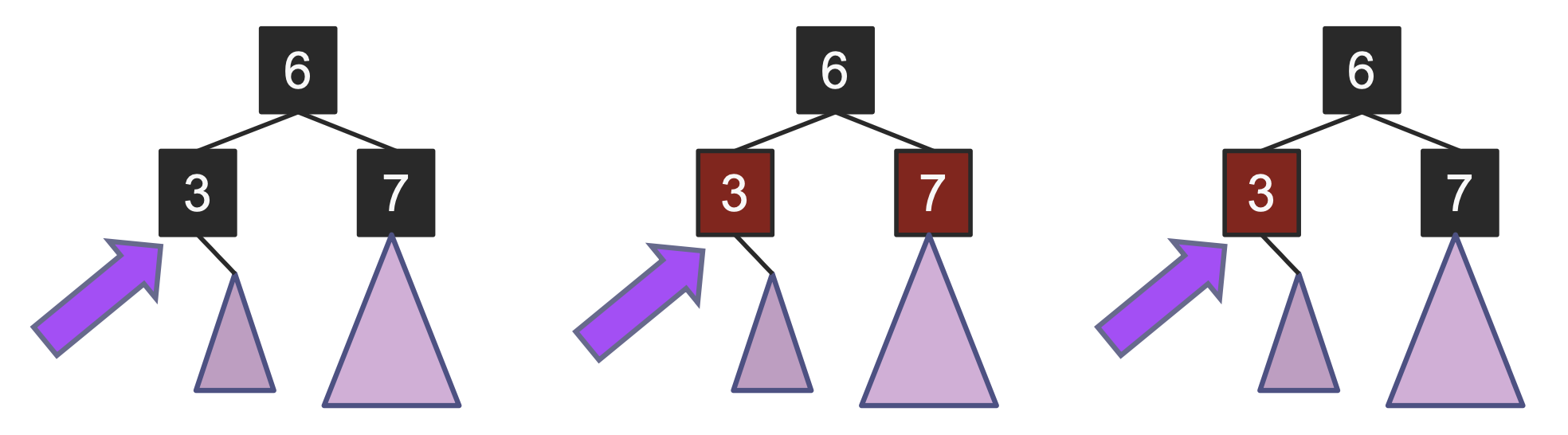
  • 이 세 가지의 경우에 대해 어떤 방식으로 삽입 연산이 일어나는지 알아보자.
  • 부모가 모두 black이면 그냥 삽입하면 된다.
  • 부모가 red이며 부모와 동일 부모를 갖는 노드가 black이라면 restructing을 수행한다.
  • 부모가 red이며 부모와 동일 부모를 갖는 노드가 red라면 recoloring을 수행한다.
• Restructing
  • 부모 노드의 부모 노드를 조상 노드라고 하자.
  • 삽입하는 노드, 부모 노드, 조상 노드를 오름차순으로 정렬한다.
  • 셋 중 중간값을 부모 노드로 설정하고, 나머지 두 값을 자식 노드로 설정한다.
  • 새로 부모가 된 노드를 black으로 만들고 나머지 자식은 red로 만든다.
• Recoloring
  • 부모 노드와 같은 부모를 가지는 노드를 삼촌 노드라고 하자.
  • 부모 노드와 삼촌 노드를 모두 black으로 변경한다. 조상 노드는 red로 변경한다.
    • 조상 노드가 루트 노드일 경우 black으로 수정한다.
    • 조상 노드가 red일때, 조상 노드의 부모 노드 역시 red라면 restructing 혹은 recoloring을 상황에 맞게 계속 진행한다.
• 시뮬레이션 사이트

reference

• B-Tree
• Red Black Tree