Sorting

Sorting

---

Sort

• record를 key값에 따라 재배치하는 것을 의미한다.
• 두 개의 key를 비교하여 sort를 수행하는 알고리즘은 아래와 같은 연산을 수행해야 한다.
  • 두 key를 비교한다.
  • key값을 복사한다.

Insertion Sort

• 배열을 sorted와 unsorted의 두 연속된 부분으로 나눈다.
• 초기값은 sorted는 빈 배열, unsorted는 전체 배열이다.
• unsorted의 첫 번째 원소를 sorted의 첫 번째 원소와 비교한다.
• sorted의 원소보다 unsorted의 원소가 작다면 해당 sorted의 왼쪽에 삽입한다.
• sorted의 원소보다 큰 경우 sorted의 원소보다 작아질 때까지 sorted의 index를 1씩 증가시키며 순회한다.
• 마지막까지 sorted의 원소보다 큰 경우 sorted의 가장 우측에 삽입한다.
• 이 과정을 unsorted의 크기가 0이 될 때까지 반복한다.
• 아래 그림은 i = 6인 상황에서의 삽입 정렬 과정을 나타낸 그림이다.
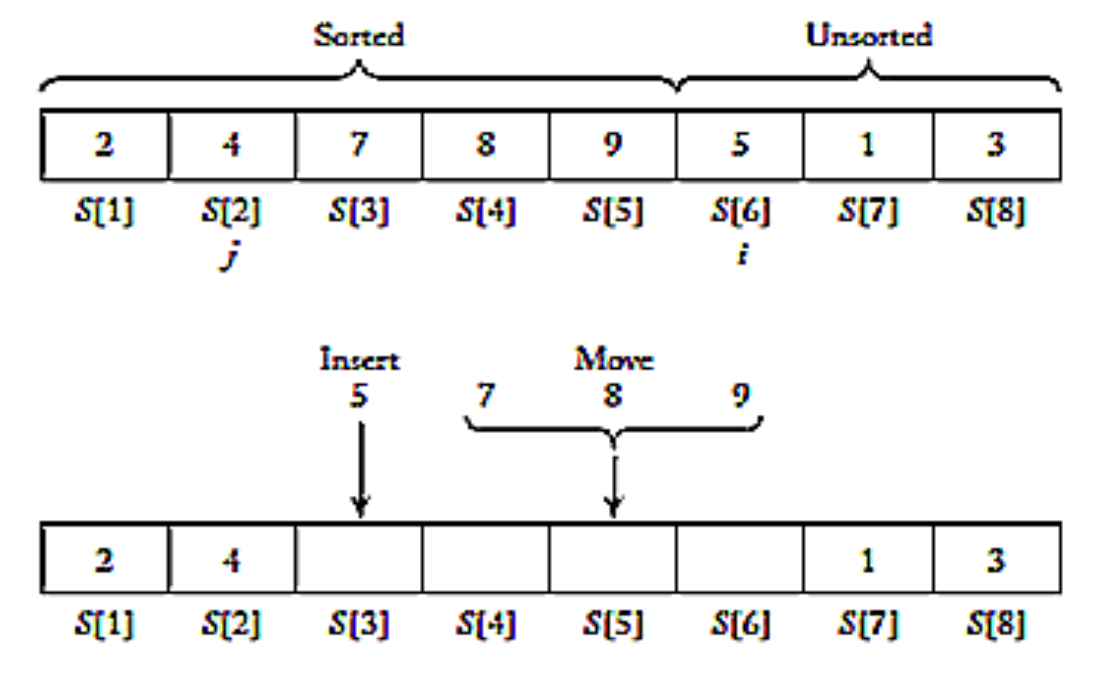
• worst case에서 quadratic의 시간복잡도를 가지는 정렬 알고리즘이다.

Exchange Sort

• 배열의 두 번째 원소부터 배열의 마지막 원소까지 배열의 첫 번째 원소와 비교하여 배열의 첫 번째 원소가 더 클 경우 두 값을 교환하는 정렬 방법이다.
• 배열의 두 번째 원소부터 시작한 교환 과정이 끝나면 배역의 세 번째 원소부터 배열의 마지막 원소까지 배열의 두 번째 원소와 비교하여 교환하는 과정을 거친다.
• 이렇게 배열의 마지막 직전 원소까지 교환이 끝나면 정렬 과정이 종료된다.
• worst case에서 quadratic의 시간복잡도를 가지는 정렬 알고리즘이다.

Selection Sort

• exchange sort방법과 유사하다.
• 배열의 첫 번째 원소부터 배열의 마지막 원소값까지의 모든 값들과 비교한다.
• 그 중 가장 작은 값과 배열의 첫 번째 원소의 값을 교환한다.
• 다시 배열의 두 번째 원소에 대해 같은 과정을 수행한다.
• 이 과정을 배열의 마지막 원소 이전까지의 원소에 대해 수행한다.
• worst case에서 quadratic의 시간복잡도를 가지는 정렬 알고리즘이다.

key값 비교의 lower bound

• n개의 서로 다른 key값으로 정렬된 집합이 있다고 하자. 편의를 위해 key값은 정수로 가정하자.
• 이 집합에서 만들어지는 순열 [k1, k2, k3, ..., kn]에 대해서 inversion은 다음과 같은 조건을 만족한다.$$(k_i, k_j) \ such\ that\ i<j\ and\ k_i > k_j$$
• 즉, [3, 2, 4, 1, 6, 5]에 대한 inversion은 (3, 2), (3, 1), (2, 1), (6, 5), (4, 1)이다.
• 이러한 inversion을 찾는 알고리즘은 아래와 같은 worst case의 경우 아래와 같은 비교연산의 횟수가 필요하다.$$\frac{n(n-1)}{2}\ comparisons\ of\ keys$$
  • [n, n-1, n-2, ..., 3, 2, 1] 순서로 정렬된 집합이 있다고 생각하자.
  • n에 대해서는 n-1번의 비교 연산이 필요하다.
  • n-1에 대해서는 n-2번의 비교 연산이 필요하다.
  • 이렇게 필요한 비교 연산을 모두 수행하면 위와 같은 비교 횟수가 필요함을 알 수 있다.
• worst case가 아닌 average case의 경우에도 아래와 같은 비교연산의 횟수가 필요하다.$$\frac{n(n-1)}{4}\ comparisons\ of\ keys$$
  • (s, r)이 서로 다른 key값의 쌍이라고 하자. 전체 집합의 원소가 n개라면 (s, r)쌍을 선택하는 것은 아래와 같다.$$the\ number\ of\ distinct\ pairs\ (i, j) = \frac{n(n-1)}{2}$$
  • key쌍의 조합에 대해 inversion일 경우는 i > j인 경우이다. average case에서 이는 1/2의 경우의 수를 가진다.
  • 따라서 average case에서는 위와 같은 비교연산의 횟수가 필요하다.

Merge Sort

• divide and conquer방식의 정렬 알고리즘이다.
• 배열을 2부분으로 계속 나눈다.
• 이렇게 생성된 모든 subarray가 크기가 1인 배열이 되면 merge를 시작한다.
• merge과정에서 key값이 작은 원소를 좌측에 배치한다.
• 각 merge과정에서 총 n번의 비교 연산을 필요로 한다.
• divide및 merge과정은 floor(log n)번 일어난다. 따라서 시간복잡도는 n * log n이다.
• 이를 의사 코드로 나타내면 아래와 같다.

  void mergesort(int n, keytype S[]) {
  	if (n>1) {
  		const int h = floor(n/2), m = n - h;
  		keytype U[1..h], V[1..m];
  		copy S[1] through S[h] to U[1] through U[h];
  		copy S[h+1] through S[n] to V[1] through V[m];
  		mergesort(h, U);
  		mergesort(m, v);
  		merge(h, m, U, V, S);
  	}
  }
  

  • copy연산의 시간복잡도는 n * log n이다.
  • merge sort에서 copy연산의 시간복잡도를 고려하면 총 시간복잡도는 2n * log n이 된다.

Improved Merge Sort

• 아래와 같이 linked list자료 구조를 사용하여 merge과정을 수행한다고 생각해 보자.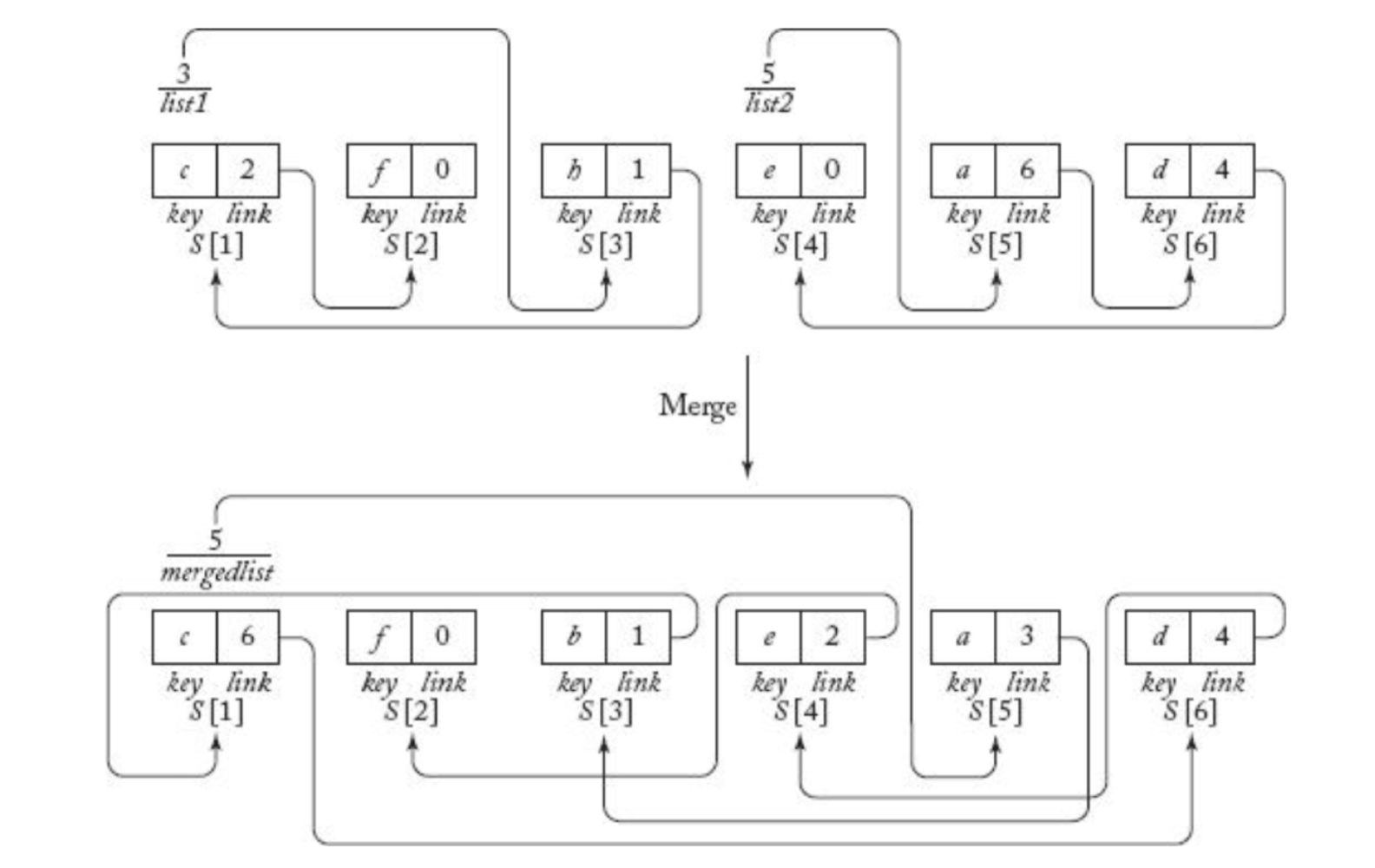
• 레코드가 정렬된 상태를 유지할 필요가 없다면 assignment 연산이 필요 없다.
• 레코드가 정렬된 상태를 유지해야 한다면 linear의 시간복잡도를 가진다.